Cho hình phẳng D giới hạn bởi đường cong y = e x - 1 cắt trục tọa độ và phần đường thẳng y = 2-x với x ≥ 1 Tính thể tích khối tròn xoay tạo thành khi quay D quanh trục hoành
![]()
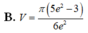
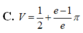
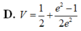
Cho hình phẳng D giới hạn đường cong y = e x − 1 , các trục tọa độ và phần đường thẳng y = 2 x với x ≥ 1. Tính thể tích khối tròn xoay tạo thành khi quay D quanh trục hoành
A. V = 1 3 + e 2 − 1 2 e 2 .
B. V = π 5 e 2 − 3 6 e 2 .
C. V = 1 2 + e − 1 e π .
D. V = 1 2 + e 2 − 1 2 e 2 .
Đáp án B.
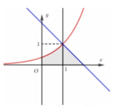
Hình phẳng D gồm 2 phần:
Phần 1: Là phần giới hạn bởi:
y = e x − 1 ; y = 0 x = 0 ; x = 1 .
Phần 2: Là phần giới hạn bởi:
y = 2 − x ; y = 0 x = 1 ; x = 2 .
Thể tích khối tròn xoay tạo thành khi quay D quanh trục hoành là:
V = π ∫ 0 1 e x − 1 2 d x + π ∫ 1 2 2 − x 2 d x = π ∫ 0 1 e 2 x − 2 d x + π ∫ 1 2 x − 2 2 d x − 2
= π e 2 x − 2 2 1 0 + π x − 2 3 3 2 1 = π e 2 − 1 2 e 2 + π 3 = π 5 e 2 − 3 6 e 2 .
Cho hình phẳng D giới hạn bởi đường cong y = ln x , trục hoành và đường thẳng x=e. Tính thể tích V của khối tròn xoay tạo thành khi quay D quanh trục hoành.
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Một vật thể có mặt đáy nằm trong mặt phẳng tọa độ (Oxy) được giới hạn bởi đường cong y 2 = 4 x và đường thẳng x = 4. Thiết diện của vật thể cắt bởi mặt phẳng vuông góc với trục Ox là một nửa hình elip có trục lớn gấp đôi trục nhỏ. Tính thể tích của vật thể.

A. 8 π
B. 16 π
C. 32 π
D. 64 π
Đáp án A
Xét thiết diện của vật thể cắt bởi mặt phẳng vuông góc với Ox tại điểm x là nửa elip có bán trục lớn bằng 2 x , do đó có bán trục nhỏ bằng x (do trục lớn gấp đôi trục nhỏ)
Suy ra diện tích của thiết diện tại điểm x là S x = 1 2 . π .2 x . x = π x
Vậy thiết diện của vật thể là V = ∫ 0 4 π x d x = π x 2 2 4 0 = 8 π . Chọn đáp án A
Một vật thể có mặt đáy nằm trong mặt phẳng tọa độ (Oxy) được giới hạn bởi đường cong y 2 = 4 x và đường thẳng x = 4. Thiết diện của vật thể cắt bởi mặt phẳng vuông góc với trục Ox là một nửa hình elip có trục lớn gấp đôi trục nhỏ. Tính thể tích của vật thể
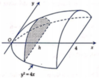
A. 8 π
B. 16 π
C. 32 π
D. 64 π
Biết diện tích hình phẳng giới hạn bởi đường cong y=f(x), y=0, x=2a bằng S. Diện tích hình phẳng giới hạn bởi đường cong y=f(2x), trục hoành Ox và hai đường thẳng x=0, x=a bằng:
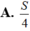
![]()
![]()
Biết diện tích hình phẳng giới hạn bởi đường cong y=f(x),y=0,x=0,x=2a bằng S. Diện tích hình phẳng giới hạn bởi đường cong y=f(2x), trục hoành Ox và hai đường thẳng x=0,x=a bằng
A. S/4.
B. 4S.
C. 2S.
D. S/2.
Cho hình phẳng (H) giới hạn bởi các đường y = x − 2 ln x + 1 , hai trục tọa độ. Diện tích S của hình phẳng (H) là
A. S = 3 − 2 ln 3.
B. S = 12 − 9 ln 3.
C. S = 4 − 9 2 ln 3.
D. S = 9 2 ln 3 − 4.
Cho (H) là hình phẳng giới hạn bởi đường cong y = x , trục hoành và đường thẳng y=2-x (phần tô đậm trong hình vẽ bên). Diện tích của (H) bằng
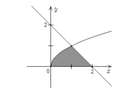
A. 4 2 - 1 3
B. 7 6
C. 8 2 + 3 6
D. 5 6
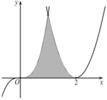
Diện tích hình phẳng giới hạn bởi parabol y = x - 2 2 , đường cong y = x 3 và trục hoành bằng (phần tô đậm trong hình vẽ bên)
A. 11 2
B. 73 12
C. 7 12
D. 5 2