Cho hàm số (m là tham số) .Gọi là hai điểm cực trị của hàm số. Tìm m để x1 1 x2. A. B. C. D.
Đọc tiếp
Cho hàm số 
(m là tham số) .Gọi 
là hai điểm cực trị của hàm số. Tìm m để x1 < 1< x2.
A. 
B. 
C. 
D. 
Những câu hỏi liên quan
Gọi x1; x2 là hai điểm cực trị của hàm số y 4x3+mx2-3x. Tìm các giá trị thực của tham số m để x1+4x20 A.
m
±
9
2
B. m±1 C. m0 D. m ±2
Đọc tiếp
Gọi x1; x2 là hai điểm cực trị của hàm số y= 4x3+mx2-3x. Tìm các giá trị thực của tham số m để x1+4x2=0
A. m = ± 9 2
B. m=±1
C. m=0
D. m= ±2
Ta có y’=12x2+2mx-3.
Do ∆ ' = m 2 + 36 > 0 , ∀ m ∈ ℝ nên hàm số luôn có hai điểm cực trị x1; x2.
Theo Viet, ta có x 1 + x 2 = - m 6 x 1 x 2 = - 1 4
Mà x1+4x2=0 suy ra
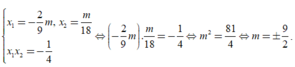
Chọn A.
Đúng 0
Bình luận (0)
Cho hàm số
y
x
3
-
3
x
2
+
m
x
-
1
với m là tham số thực. Tìm tất cả các giá trị của tham số m để hàm số đạt cực trị tại hai điểm
x
1
,
x
2
thỏa
x
1
2...
Đọc tiếp
Cho hàm số y = x 3 - 3 x 2 + m x - 1 với m là tham số thực. Tìm tất cả các giá trị của tham số m để hàm số đạt cực trị tại hai điểm x 1 , x 2 thỏa x 1 2 + x 2 2 = 6 .
A. 3.
B. -1.
C. 1.
D. -3.
Gọi
x
1
,
x
2
là hai điểm cực trị của hàm số
y
x
3
-
3
m
x
2
+
3
(...
Đọc tiếp
Gọi x 1 , x 2 là hai điểm cực trị của hàm số y = x 3 - 3 m x 2 + 3 ( m 2 - 1 ) x - m 3 + m . Tìm tất cả các giá trị của tham số thực m để : x 1 2 + x 2 2 - x 1 x 2 = 7
A. m = ± 2 .
B. m = ± 2 .
C. m = 0 .
D. m = ± 1 .
Chọn B
[Phương pháp tự luận]
y ' = 3 x 2 - 6 m x + 3 ( m 2 - 1 )
Hàm số luôn luôn có cực trị với moi m
Theo định lí Viet
x 1 + x 2 = 2 m x 1 . x 2 = m 2 - 1
x 1 2 + x 2 2 - x 1 x 2 = 7
⇔ ( 2 m ) 2 - 3 ( m 2 - 1 ) = 7
⇔ m = ± 2
Đúng 0
Bình luận (0)
Cho hàm số y x4-2( m+1)x2+ m ( C). Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số C có ba điểm cực trị A: B; C sao cho OA BC ; trong đó O là gốc tọa độ, A là điểm cực trị thuộc trục tung, B và C là hai điểm cực trị còn lại. A.
m
2
±
2
2
B.
m
2
+
2
2
C.
m
2...
Đọc tiếp
Cho hàm số y= x4-2( m+1)x2+ m ( C). Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số C có ba điểm cực trị A: B; C sao cho OA= BC ; trong đó O là gốc tọa độ, A là điểm cực trị thuộc trục tung, B và C là hai điểm cực trị còn lại.
A. m = 2 ± 2 2
B. m = 2 + 2 2
C. m = 2 - 2 2
D. m = ± 1
Ta có : y’ = 4x3-4( m+ 1) x= 4x( x2- (m+ 1) ).
Hàm số có điểm cực trị khi và chỉ khi y’ = 0 có nghiệm phân biệt hay m+1> 0 suy ra m> - 1. (*)
Khi đó, ta có:
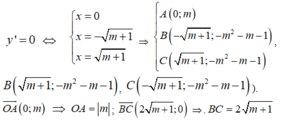
Do đó O A = B C ⇔ m = 2 m + 1 ⇔ m 2 - 4 m - 4 = 0 ( ∆ ' = 8 ) ⇔ m = 2 ± 2 2 (thỏa mãn (*)).
Vậy m = 2 ± 2 2 .
Chọn A.
Đúng 0
Bình luận (0)
Cho hàm số
y
x
4
-
2
(
m
+
1
)
x
2
+
m
(
C
)
. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số (C) có b...
Đọc tiếp
Cho hàm số y = x 4 - 2 ( m + 1 ) x 2 + m ( C ) . Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số (C) có ba điểm cực trị A, B, C sao cho OA = BC; trong đó O là gốc tọa độ, A là điểm cực trị thuộc trục tung, B và C là hai điểm cực trị còn lại
A. m = 2 ± 2 2
B. m = 2 + 2 2
C. m = 2 - 2 2
D. m = ± 1
Chọn A
Ta có:
Hàm số có 3 điểm cực trị khi và chỉ khi :
y ' có 3 nghiệm phân biệt
⇔ m + 1 > 0 ⇔ m > - 1 ( * )
Khi đó, ta có y ' = 0
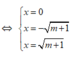
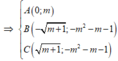
(vai trò của B, C trong bài toán là như nhau ) nên ta giả sử
Ta có: O A ( 0 ; m ) ⇒ O A = m ⇒ B C = 2 m + 1
Do đó OA = BC
⇔ m = 2 ± 2 2 ( t h ỏ a m ã n ) ( * )
Vậy m = 2 ± 2 2
Đúng 0
Bình luận (0)
Cho hàm số
y
m
3
x
3
+
(
m
-
2
)
x
2
+
(
m
-
1
)
x
+
2
, với
m
là tham số thực. Tìm tất cả các giá trị thực của tham số
m
sao cho hàm số đạt cực đại tại điểm
x
1
và đạt...
Đọc tiếp
Cho hàm số y = m 3 x 3 + ( m - 2 ) x 2 + ( m - 1 ) x + 2 , với m là tham số thực. Tìm tất cả các giá trị thực của tham số m sao cho hàm số đạt cực đại tại điểm x 1 và đạt cực tiểu tại điểm x 2 thỏa mãn x 1 < x 2
A. 0 < m < 4 3
B. m ≤ 0
C. 5 4 < m < 4 3
D. Không tồn tại m thỏa mãn
Cho hàm số
y
m
3
x
3
+
m
-
2
x
2
+
m
-
1
x
, với m là tham số thực. Tìm tất cả các giá trị thực của tham số m sao cho hàm số đạt cực đại tại điểm
x
1
và đạt cực tiểu...
Đọc tiếp
Cho hàm số y = m 3 x 3 + m - 2 x 2 + m - 1 x , với m là tham số thực. Tìm tất cả các giá trị thực của tham số m sao cho hàm số đạt cực đại tại điểm x 1 và đạt cực tiểu tại điểm x 2 thỏa mãn x 1 < x 2
A. 0 < m < 4 3
B. m ≤ 0
C. 5 4 < m < 4 3
D. Không tồn tại m
Chọn A.
Phương pháp : Sử dụng đạo hàm và đặc trưng cực trị hàm số đa thức bậc ba.
Đúng 0
Bình luận (0)
Cho hàm số
f
x
1
3
x
3
−
m
x
+
2
, m là tham số. Biết hàm số có hai điểm cực trị
x
1
,
x
2
. Tìm giá trị nhỏ nhất của biểu thức
T
x
1
2
+
x
2...
Đọc tiếp
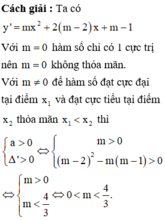
Cho hàm số f x = 1 3 x 3 − m x + 2 , m là tham số. Biết hàm số có hai điểm cực trị x 1 , x 2 . Tìm giá trị nhỏ nhất của biểu thức T = x 1 2 + x 2 2 − 10 x 1 + x 2
A. -1
B. 1
C. -18
D. -22
Đáp án D
Ta có: f ' x = x 2 − 2 m + 1 x − 2 m + 1
Hàm số có 2 điểm cực trị ⇔ Δ ' = m + 1 2 + 8 m − 4 = m 2 + 12 m − 3 > 0 *
Khi đó gọi x 1 ; x 2 là hoành độ các điểm cực trị ta có: x 1 + x 2 = 2 m + 2 x 1 x 2 = − 2 m + 1
Khi đó: T = x 1 + x 2 2 − 10 x 1 + x 2 − 2 x 1 x 2 = 2 m + 2 2 − 10 2 m + 2 + 4 m − 2
⇔ T = 4 m 2 − 8 m − 18 = 4 m − 1 2 − 22 ≥ − 22 . dấu bằng xảy ra ⇔ m = 1 t / m *
Đúng 0
Bình luận (0)
Cho hàm số
y
x
3
+
2
m
−
2
x
2
−
5
x
+
1
. Tìm tất cả các giá trị thực của tham số m sao cho hàm số có hai điểm cực trị
x
1
,
x
2
(
x
1...
Đọc tiếp
Cho hàm số y = x 3 + 2 m − 2 x 2 − 5 x + 1 . Tìm tất cả các giá trị thực của tham số m sao cho hàm số có hai điểm cực trị x 1 , x 2 ( x 1 < x 2 ) thỏa mãn x 1 − x 2 = − 2 .
A. 7 2
B. ‒1
C. 1 2
D. 5
Đáp án C.
Ta có y ' = 3 x 2 + 4 m − 2 x − 5 ; y ' = 0 ⇔ 3 x 2 + 4 m − 2 x − 5 = 0 (*).
Phương trình (*) có a c < 0 nên luôn có hai nghiệm trái dấu .
Suy ra x 1 = − x 1 ; x 2 = x 2 .
Khi đó x 1 , x 2 là hai điểm cực trị của hàm số.
x 1 − x 2 = − 2 ⇔ − x 1 − x 2 = − 2 ⇔ x 1 + x 2 = 2 ⇔ − 4 m − 2 3 = 2 ⇔ m = 1 2
Đúng 0
Bình luận (0)