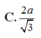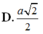Bán kính của mặt cầu ngoại tiếp hình chóp đều S.ABC có tất cả các cạnh bằng a là
Đọc tiếp
Bán kính của mặt cầu ngoại tiếp hình
chóp đều S.ABC có tất cả các cạnh
bằng a là
Những câu hỏi liên quan
Bán kính của mặt cầu ngoại tiếp chóp đều S.ABC có tất cả cac cạnh bằng a là:
A
.
3
a
6
4
B
.
a
6
12
C
.
a
6
4
D...
Đọc tiếp
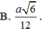
Bán kính của mặt cầu ngoại tiếp chóp đều S.ABC có tất cả cac cạnh bằng a là:
A . 3 a 6 4
B . a 6 12
C . a 6 4
D . a 6 4
Hình chóp tứ giác đều có tất cả các cạnh bằng a. Tính bán kính R của mặt cầu ngoại tiếp hình chóp. A. R a B. R
a
2
C. R
a
2
2
D. R
a
3
2
Đọc tiếp
Hình chóp tứ giác đều có tất cả các cạnh bằng a. Tính bán kính R của mặt cầu ngoại tiếp hình chóp.
A. R = a
B. R = a 2
C. R = a 2 2
D. R = a 3 2
Cho hình chóp đều S.ABC có cạnh đáy bằng a, góc tạo bởi cạnh bên với đáy bằng
60
°
. Bán kính R mặt cầu ngoại tiếp hình chóp S.ABC là A.
R
a
2
B.
R
2
a
3
C.
R
a
3
3
D.
R...
Đọc tiếp
Cho hình chóp đều S.ABC có cạnh đáy bằng a, góc tạo bởi cạnh bên với đáy bằng 60 ° . Bán kính R mặt cầu ngoại tiếp hình chóp S.ABC là
A. R = a 2
B. R = 2 a 3
C. R = a 3 3
D. R = 4 a 3
Cho hình chóp S.ABC có SA
a
3
2
, các cạnh còn lại cùng bằng a. Bán kính R của mặt cầu ngoại tiếp hình chóp S.ABC là:
Đọc tiếp
Cho hình chóp S.ABC có SA= a 3 2 , các cạnh còn lại cùng bằng a. Bán kính R của mặt cầu ngoại tiếp hình chóp S.ABC là:
Cho hình chóp S.ABC có
S
A
a
3
2
, các cạnh còn lại cùng bằng a. Bán kính R của mặt cầu ngoại tiếp hình chóp S.ABC là: A.
R
a
13
2
B.
R
a
3
C.
R
a...
Đọc tiếp
Cho hình chóp S.ABC có S A = a 3 2 , các cạnh còn lại cùng bằng a. Bán kính R của mặt cầu ngoại tiếp hình chóp S.ABC là:
A. R = a 13 2
B. R = a 3
C. R = a 13 3
D. R = a 13 6
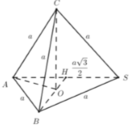
Ta có C A = C B = C S = a Hình chiếu của C trên (SAB) trùng với tâm đường tròn ngoại tiếp ∆ S A B .
Gọi O là tâm đường tròn ngoại tiếp ∆ S A B ⇒ S O ⊥ S A B .
Gọi H là trung điểm của SA. Tam giác SAB cân tại B ⇒ B H ⊥ S A ⇒ O ∈ B H .
Ta có:
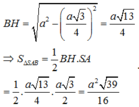
Gọi R là bán kính ngoại tiếp
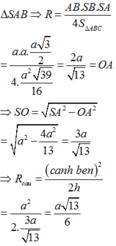
Chọn D.
Đúng 0
Bình luận (0)
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng 2a. Tính bán kính R của mặt cầu ngoại tiếp hình chóp đã cho. A.
R
a
3
2
B.
R
a
2
4
C.
R
a
2
D.
R
a...
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng 2a. Tính bán kính R của mặt cầu ngoại tiếp hình chóp đã cho.
A. R = a 3 2
B. R = a 2 4
C. R = a 2
D. R = a 2 2
Chọn C.
Phương pháp:
Xác định tâm mặt cầu ngoại tiếp hình chóp đều là giao của đường trung trực 1 cạnh bên và chiều cao của hình chóp.
Từ đó sử dụng tam giác đồng dạng để tính bán kính mặt cầu ngoại tiếp hình chóp đều.
Cách giải:
Đúng 0
Bình luận (0)
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng 2a. Tính bán kính R của mặt cầu ngoại tiếp hình chóp đã cho.
Đọc tiếp
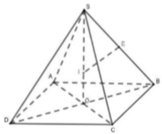
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng 2a. Tính bán kính R của mặt cầu ngoại tiếp hình chóp đã cho.
Cho hình chóp tứ giác đều có tất cả các cạnh bằng 2a. Bán kính mặt cầu ngoại tiếp hình chóp đã cho bằng A.
a
6
2
B.
a
2
C.
2
a
3
D.
a
2
2
Đọc tiếp
Cho hình chóp tứ giác đều có tất cả các cạnh bằng 2a. Bán kính mặt cầu ngoại tiếp hình chóp đã cho bằng
A. a 6 2
B. a 2
C. 2 a 3
D. a 2 2
Chon B.
Phương pháp:
Xác định trục của khối chóp sau đó dựng đường thẳng trung trực của một cạnh bên của khối chóp để tìm được tâm của mặt cầu. Từ đó tính bán kính mặt cầu.
Cách giải:
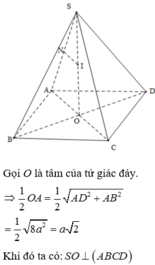
=>SO là trục của đường tròn ngoại tiếp tứ giác ABCD.
Trong mặt phẳng (SOA), vẽ đường trung trực của cạnh SA, cắt SO tại I.
=>I là tâm mặt cầu ngoại tiếp hình chóp.
Ta có:
Đúng 0
Bình luận (0)
Cho hình chóp tứ giác đều có tất cả các cạnh bằng 2a. Bán kính mặt cầu ngoại tiếp hình chóp đã cho bằng
Đọc tiếp
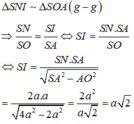
Cho hình chóp tứ giác đều có tất cả các cạnh bằng 2a. Bán kính mặt cầu ngoại tiếp hình chóp đã cho bằng
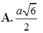
