Cho hình lăng trụ đứng ABC.A' B' C' có AB=AC=a, góc ∠ BAC = 120 0 , AA ' = a .Gọi M, N lần lượt là trung điểm của B^' C^' và CC^'. Số đo góc giữa mặt phẳng (AMN) và mặt phẳng (ABC) bằng:
A. 60 0
B. 30 0
C. arcsin 3 4
D. arccos 3 4
Cho hình lăng trụ đứng tam giác ABC.A′B′C′, tam giác ABC có AB = a , AC = a 2 , góc BAC ^ = 60 0 , A ' C = a 3 . Tính thể tích khối lăng trụ ABC.A′B′C′ là
A. a 3 6 2
B. a 3 3 4
C. a 3 3 6
D. a 3 6 4
Cho lăng trụ đứng ABC.A′B′C′ có đáy là tam giác cân, AB = AC = 2 a , BAC ^ = 120 ° . Mặt phẳng AB ' C ' tạo với đáy một góc 60 ° . Thể tích khối lăng trụ bằng
A. a 3 2 (dvtt)
B. a 3 (dvtt)
C. a 3 6 (dvtt)
D. 3 a 3 (dvtt)
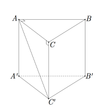
Cho hình lăng trụ đứng ABC.A′B′C′ có đáy là tam giác vuông tại A,AB= a 3 ,AC=AA'=a. Sin góc giữa đường thẳng AC′ và mặt phẳng (BCC′B′) bằng
A. 3 3
B. 10 4
C. 10 4
D. 6 4
Cho hình lăng trụ đứng ABC.A'B'C' có AA'=AB=AC=1, B A C ^ = 120 ° Gọi M là trung điểm cạnh CC′. Côsin góc giữa hai mặt phẳng (ABC) và (AB′M) bằng
A. 30 10
B. 70 10
C. 30 20
D. 370 20
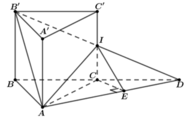
Cho hình lăng trụ đứng ABC.A'B'C' có A A ' = A B = A C = 1 và B A C ^ = 120 ° . Gọi I là trung điểm cạnh CC'. Côsin góc giữa hai mặt phẳng (ABC) và (AB'I) bằng
A. 30 10
B. 70 10
C. 30 20
D. 370 20
Gọi ![]()
Khi đó ![]()
Ta tính được ![]()
![]()
Ta có
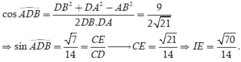
Vậy 
Chọn A.
Cách 2. Vì
∆
ABC là hình chiếu của
∆
AB'I trên mp (ABC) nên 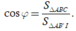
Cho lăng trụ đứng ABC.A'B'C' có cạnh bên AA'=2a,AB=AC =a, góc B A C ^ = 120 ° . Gọi M là trung điểm của BB' thì cosin của góc tạo bởi hai mặt phẳng (ABC) và (AC'M) là:
A. 3 31
B. 5 5
C. 3 15
D. 93 31
Đáp án D
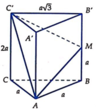
Nhận thấy ∆ A B C là hình chiếu của ∆ A M C ' lên mặt phẳng (ABC).
Gọi φ là góc giữa (AMC') và ( A B C ) ⇒ S ∆ A B C = S ∆ A M C ' . cos φ ⇒ cos φ = S ∆ A B C S ∆ A M C '
Ta có S ∆ A B C = 1 2 a 2 . sin 120 ° = a 2 3 4
A ' C = a 5 ; A M = a 2 ; B C = a 2 + a 2 - 2 a cos 120 ° = a 3 ⇒ C ' M = 2 a
Đặt p = a 5 + a 2 + 2 a 2
⇒ S ∆ A M C ' = p ( p - a 2 ) ( p - a 5 ) ( p - 2 a ) = 31 4 a 2
⇒
cos
φ
=
a
2
3
4
.
4
31
a
2
=
3
31
=
93
31
Cho lăng trụ đứng ABC. A’B’C’ có cạnh bên AA’=2a, AB=AC=a, góc B A C ^ = 120 ° . Gọi M là trung điểm của BB’ thì cosin của góc tạo bởi hai mặt phẳng (ABC) và (AC’M) là
A. 3 31
B. 3 3
C. 3 15
D. 93 31
Cho lăng trụ đứng ABC.A′B′C′ có đáy là tam giác cân, AB = AC = 2a, B A C ^ = 120 o Mặt phẳng (AB′C′) tạo với đáy một góc 60o . Thể tích khối lăng trụ bằng
![]()
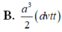
![]()
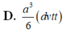
Chọn A
Gọi I là trung điểm của B′C′.Trong tam giác A′B′C′
ta có

![]()
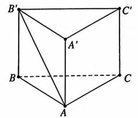
Cho hình lăng trụ đứng tam giác ABC.A'B'C' có đáy ABC là tam giác cân, AB=AC=a, B A C ^ = 120 ∘ , cạnh bên A A ' = a 2 . Tính góc giữa hai đường thẳng AB' và BC. (tham khảo hình vẽ bên)
A. 90 ∘
B. 30 ∘
C. 45 ∘
D. 60 ∘