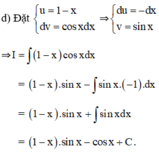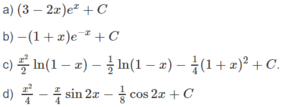Sử dụng phương pháp tính nguyên hàm từng phần, hãy tính: ∫ x 2 + 2 x - 1 . e x d x

Những câu hỏi liên quan
Sử dụng phương pháp tính nguyên hàm từng phần, hãy tính: ∫ x . ln 1 + x d x
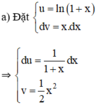
Theo công thức nguyên hàm từng phần ta có:
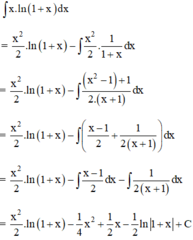
Đúng 0
Bình luận (0)
Sử dụng phương pháp tính nguyên hàm từng phần, hãy tính: ∫ 1 - x . cos x d x
Áp dụng phương pháp tính nguyên hàm từng phần, hãy tính: ∫ x ln ( 1 - x ) d x
x 2 2 ln 1 - x - 1 2 ln 1 - x - 1 4 1 + x 2 + C
Đúng 0
Bình luận (0)
Hãy tính ∫ x + 1 e x d x bằng phương pháp tính nguyên hàm từng phần.
Áp dụng phương pháp tính nguyên hàm từng phần, hãy tính:
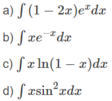
Áp dụng phương pháp tính nguyên hàm từng phần, hãy tính: ∫ x sin 2 x d x
x 2 4 - x 4 sin 2 x - 1 8 c o s 2 x + C
HD: Đặt u = x, dv = sin 2 x dx
Đúng 0
Bình luận (0)
Áp dụng phương pháp tính nguyên hàm từng phần, hãy tính: ∫ 1 - 2 x e x d x
Áp dụng phương pháp tính nguyên hàm từng phần, hãy tính: ∫ x e - x d x
Để tính
∫
xln
(
2
+
x
)
.
dx
theo phương pháp tính nguyên hàm từng phần, ta đặt: A.
u
v
d
v
ln
2...
Đọc tiếp
Để tính ∫ xln ( 2 + x ) . dx theo phương pháp tính nguyên hàm từng phần, ta đặt:
A. u = v d v = ln 2 + x d x
B. u = ln 2 + x d v = x d x
C. u = x ln 2 + x d v = d x
D. u = ln 2 + x d v = d x
Chọn B.
Chú ý: “ Nhất log, nhì đa, tam lượng, tứ mũ”.
Đúng 0
Bình luận (0)