Đặt
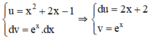
Theo công thức nguyên hàm từng phần ta có:
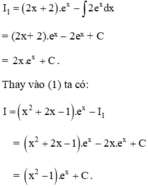
Đặt
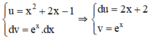
Theo công thức nguyên hàm từng phần ta có:
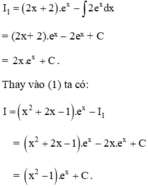
Áp dụng phương pháp tính nguyên hàm từng phần, hãy tính: ∫ x ln ( 1 - x ) d x
Sử dụng phương pháp tính nguyên hàm từng phần, hãy tính: ∫ 1 - x . cos x d x
Hãy tính ∫ x + 1 e x d x bằng phương pháp tính nguyên hàm từng phần.
Sử dụng phương pháp tính nguyên hàm từng phần, hãy tính: ∫ x . ln 1 + x d x
Để tính ∫ xln ( 2 + x ) . dx theo phương pháp tính nguyên hàm từng phần, ta đặt:
A. u = v d v = ln 2 + x d x
B. u = ln 2 + x d v = x d x
C. u = x ln 2 + x d v = d x
D. u = ln 2 + x d v = d x
Để tính ∫ x ln ( 2 + x ) d x theo phương pháp tính nguyên hàm từng phần, ta đặt:
A. u = v d v = ln 2 + x d x
B. u = ln 2 + x d v = x d x
C. u = x ln 2 + x d v = d x
D. u = ln 2 + x d v = d x
Áp dụng phương pháp tính nguyên hàm từng phần, hãy tính: ∫ 1 - 2 x e x d x
Áp dụng phương pháp tính nguyên hàm từng phần, hãy tính:
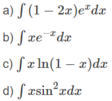
Áp dụng phương pháp tính nguyên hàm từng phần, hãy tính: ∫ x sin 2 x d x