Cho hàm số y = x3 – 3x2 + 1 (C). Tìm tổng hoành độ của hai điểm A; B trên đồ thị hàm số sao cho tiếp tuyến của đồ thị (C) tại A; B song song với nhau và A B = 4 2
A: 1
B: 2
C: 3
D: 5
Những câu hỏi liên quan
Tìm hệ số góc tiếp tuyến của đồ thị hàm số
y
−
x
3
−
3
x
2
+
2
tại điểm có hoành độ là nghiêṃ của phương trình y ¢¢ 0 A. 3 B. 2 C. 1 D. 4
Đọc tiếp
Tìm hệ số góc tiếp tuyến của đồ thị hàm số y = − x 3 − 3 x 2 + 2 tại điểm có hoành độ là nghiêṃ của phương trình y ¢¢ = 0
A. 3
B. 2
C. 1
D. 4
Đáp án A
Hệ số góc của tiếp tuyến của đồ thị hàm số chính là đạo hàm cấp 1
Ta có y = − x 3 − 3 x 2 + 2 ⇒ y ' = − 3 x 2 − 6 x ⇒ y ' ' = − 6 x − 6
Phương trình y ' ' = 0 ⇔ x = − 1
Vậy hệ số góc cần tìm là k = y ' 1 = 3
Đúng 0
Bình luận (0)
Số giao điểm của đồ thị hàm số y = x 3 - 3 x 2 + 2 x + 1 với trục hoành là
A. 0
B. 1
C. 2
D. 4
Cho y=-2.x
a)tìm tung độ của điểm A biết hoành độ của điểm A=2
b)Điểm M thuộc đồ thị có tung độ bằng -2, tìm hoành độ
Cho hàm số
y
x
3
-
3
x
2
+
m
-
1
x
-
m
(m là tham số). Tìm m tham số ra để đồ thị của hàm số có hai điểm cực trị đối xứng nhau qua điểm
A
-
1
;
3
? A. m4 B. m6 C. m4 D. m6
Đọc tiếp
Cho hàm số y = x 3 - 3 x 2 + m - 1 x - m (m là tham số). Tìm m tham số ra để đồ thị của hàm số có hai điểm cực trị đối xứng nhau qua điểm A - 1 ; 3 ?
A. m>4
B. m<6
C. m<4
D. m>6
Cho đồ thị hàm số
y
x
3
-
2
x
2
+
2
x
.
Gọi
x
1
,
x
2
là hoành độ các điểm M, N trên (C) mà tại đó tiếp tuyến của (C) vuông góc với đường thẳng y -x + 2016. Khi đó
x
1
+
x
2
bằng: A.
4
3...
Đọc tiếp
Cho đồ thị hàm số y = x 3 - 2 x 2 + 2 x . Gọi x 1 , x 2 là hoành độ các điểm M, N trên (C) mà tại đó tiếp tuyến của (C) vuông góc với đường thẳng y = -x + 2016. Khi đó x 1 + x 2 bằng:
A. 4 3
B. - 4 3
C. 1 3
D. -1
Ta có y ' = 3 x 2 - 4 x + 2
Do tiếp tuyến của (C) vuông góc với đường thẳng y = -x + 2016 nên hệ số góc của tiếp tuyến là k = 1
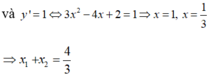
Chọn A
Đúng 0
Bình luận (0)
Cho đồ thị hàm số
y
x
3
+
3
x
2
-
2
có các điểm cực đại A(-2;2) và điểm cực tiểu B(0;-2) thì phương trình
x
3
+
3
x
2
-
2
m
có hai nghiệm khi A.
-
2
m
2
B.
m
-
2
hoặc
m...
Đọc tiếp
Cho đồ thị hàm số y = x 3 + 3 x 2 - 2 có các điểm cực đại A(-2;2) và điểm cực tiểu B(0;-2) thì phương trình x 3 + 3 x 2 - 2 = m có hai nghiệm khi
A. - 2 < m < 2
B. m = - 2 hoặc m = 2
C. m > 2
D. m < - 2
Cho hàm số
y
x
3
-
3
x
2
-
6
x
+
8
(C). Phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số (C) là: A. y 6x – 6 B. y -6x – 6 C. y 6x + 6 D. y -6x + 6
Đọc tiếp
Cho hàm số y = x 3 - 3 x 2 - 6 x + 8 (C). Phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số (C) là:
A. y = 6x – 6
B. y = -6x – 6
C. y = 6x + 6
D. y = -6x + 6
Chọn D
Cách 1: Ta có y ’ = 3 x 2 - 6 x - 6 ; y ” = 6 x - 6
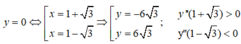
Do đó đồ thị hàm số có điểm cực trị là A ( 1 + 3 ; - 6 3 ) và B ( 1 - 3 ; 6 3 ) .
Phương trình đường thẳng đi qua hai điểm cực trị là:
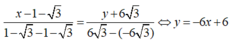
Cách 2: Ta có:
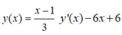
Gọi x 1 , x 2 là nghiệm của phương trình y ’ ( x ) = 3 x 2 - 6 x - 6 = 0 . Khi đó ta có A ( x 1 , y ( x 1 ) ) , B A ( x 2 , y ( x 2 ) ) là hai cực trị của đồ thị hàm số C với y ' ( x 1 ) = y ' ( x 2 ) = 0 .
Do đó ta có:
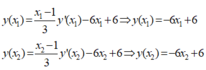
Vậy A, B thuộc đường thẳng y= - 6x+6.
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị của tham số m để hàm số
y
x
3
-
3
x
2
+
m
x
+
1
có hai điểm cực trị A.
m
≤
3
B.
m
3
C.
m
-
3
D.
m
3
Đọc tiếp
Tìm tất cả các giá trị của tham số m để hàm số y = x 3 - 3 x 2 + m x + 1 có hai điểm cực trị
A. m ≤ 3
B. m > 3
C. m > - 3
D. m < 3
Cho hàm số
y
x
3
-
3
x
2
+
m
x
-
1
với m là tham số thực. Tìm tất cả các giá trị của tham số m để hàm số đạt cực trị tại hai điểm
x
1
,
x
2
thỏa
x
1
2...
Đọc tiếp
Cho hàm số y = x 3 - 3 x 2 + m x - 1 với m là tham số thực. Tìm tất cả các giá trị của tham số m để hàm số đạt cực trị tại hai điểm x 1 , x 2 thỏa x 1 2 + x 2 2 = 6 .
A. 3.
B. -1.
C. 1.
D. -3.
