Tính đạo hàm đến cấp đã chỉ ra của hàm số sau: 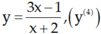
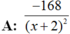
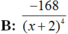
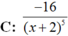
Tính đạo hàm đến cấp đã chỉ ra của hàm số sau: y = cos2x,(y’’’)
A: sin2x
B: 2 sin2x
C: sin 4x
D: 4sin2x
Tính đạo hàm đến cấp đã chỉ ra của hàm số sau: y = xsin2x,(y’’’)
A. -12sinx - 8cos 2x
B. -12sin2x + 8cos2x
C.12sin2x - 8cos2x
D. -12sin2x -8 cos2x.
Chọn D.
Có y’ = x’sin2x + x.(sin2x)’ = sin2x + 2xcos2x
⇒ y’’ = (sin2x)’ + (2x)’cos2x + 2x(cos2x)’ = 4cos2x – 4xsin2x
⇒ y’’’ = 4(cos2x)’ – (4x)’sin2x – 4x(sin2x)’ = -8sin2x – 4sin2x – 8cos2x
= -12sin2x – 8cos2x.
Tính đạo hàm đến cấp đã chỉ ra của hàm số sau: y = x4 – sin2x, (y(4))
A: 16 - 8sin 2x
B: 24 - 8sin2x
C: 24 - 16sin2x
D: 16 - 24sin2x
Chọn C.
y = x4 - sin2x
⇒ y’ = 4x3 – 2cos2x ⇒ y’’ = 12x2 + 4sin2x
⇒ y’’’ = 24x + 8cos2x ⇒ y(4) = 24 – 16sin2x
Cho hàm số y = 1 x − 3 . Tính đạo hàm cấp hai của hàm số đã cho tại x = 1?
A. y " ( 1 ) = − 1 4
B. y " ( 1 ) = 1 4
C. y " ( 1 ) = 1 6
D. y " ( 1 ) = − 1 6
Đáp án A
Ta có: y ' = − 1 ( x − 3 ) 2 . ( x − 3 ) ' = − 1 ( x − 3 ) 2 y " = − 1 ( x − 3 ) 2 ' = − − 1 ( x − 3 ) 4 = 1 ( x − 3 ) 4 .2 ( x − 3 ) = 2 ( x − 3 ) 3 ;
⇒ y " ( 1 ) = 2 ( 1 − 3 ) 3 = − 1 4 .
Tính (bằng định nghĩa) đạo hàm của mỗi hàm số tại các điểm đã chỉ ra: y = 1 x tại x 0 = 2
Tính ( bằng định nghĩa) đạo hàm của mỗi hàm số tại các điểm đã chỉ ra: y = x 2 + x tại x 0 = 1
Tính (bằng định nghĩa) đạo hàm của mỗi hàm số tại các điểm đã chỉ ra: y = x + 1 x - 1 tại x 0 = 0
Tính đạo hàm cấp hai của các hàm số sau: y = tan x
Tính đạo hàm cấp hai của các hàm số sau: y = xcos2x
A: -4sin2x
B: -4x.cos2x
C: -4sin2x - 4x.cos2x
D: 4sin2x + 4x.cos2x
Chọn C.
y' = cos2x – 2xsin2x;
y” = -2sin2x – (2sin2x + 4xcos2x) = -4sin2x – 4xcos2x.