B. Phần tự luận (7 điểm)
Cho tam giác ABC vuông tại A có ∠ B = 50 o
a. So sánh AB và AC
Những câu hỏi liên quan
B. Phần tự luận (7 điểm)Cho tam giác ABC có
A
B
6
c
m
,
A
C
8
c
m
,
B
C
10
c
m
a. So sánh ba góc của tam giác ABC. Tam giác ABC là tam giác gì? Vì sao
Đọc tiếp
B. Phần tự luận (7 điểm)
Cho tam giác ABC có A B = 6 c m , A C = 8 c m , B C = 10 c m
a. So sánh ba góc của tam giác ABC. Tam giác ABC là tam giác gì? Vì sao
a. Do BC > AC > AB ⇒ ∠A > ∠B > ∠C
Ta có AB2 + AC2 = 62 + 82 = 100 = 102 = BC2
Vậy tam giác ABC vuông tại A (1 điểm)
Đúng 0
Bình luận (0)
B. Phần tự luận (7 điểm)
Cho tam giác ABC vuông tại A có AB = 6cm, AC = 8cm.
a. Tính độ dài cạnh BC
a. Áp dụng định lí Pytago trong tam giác ABC ta có:
BC2 = AB2 + AC2 = 62 + 82 = 100 ⇒ BC = 10cm
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có góc B=50° a,so sánh AB và AC b,kẻ Ah vuông góc với BC tại h so sánh Bh và AB khi BC=2AB
giác ABC vuông tại A có góc B bằng 50 độ a so sánh AB và AC B kẻ đường phân giác BD của góc ABC kẻ dh vuông góc với BC Chứng minh tam giác hde cân C Gọi K là giao điểm của AB và AC
Đọc tiếp
giác ABC vuông tại A có góc B bằng 50 độ a so sánh AB và AC B kẻ đường phân giác BD của góc ABC kẻ dh vuông góc với BC Chứng minh tam giác hde cân C Gọi K là giao điểm của AB và AC
a: góc C=90-50=40 độ
Vì góc B>góc C
nên AC>AB
b: Sửa đề: CM ΔADH cân tại D
Xet ΔBAD vuông tại A và ΔBHD vuông tại H có
BD chung
góc ABD=góc HBD
=>ΔBAD=ΔBHD
=>DA=DH
=>ΔDAH cân tại D
Đúng 0
Bình luận (0)
1)So sánh các cạnh của Tam giác ABC biết A 80° B40°2)Sosánh các cạnh của Tam giác PQR biết P 70° R 50°3) Cho tam giác ABC vuông tại A , điểm K nằm giữa A và C . So sánh độ dài BK và BC 4) cho tam giác MNP vuông tại N . Trên tia đối của tia PN lấy điểm Q . So sánh độ dài MP và MQ5) Cho tam giác ABC có ba góc nhọn AB AC . Kẻ BD vuông góc với AC tại D , CD vuông góc với AB tại E . Gọi H là giao điểm của BC và CE . So sánh độ dài của HB và HC
Đọc tiếp
1)So sánh các cạnh của Tam giác ABC biết A= 80° B=40°
2)Sosánh các cạnh của Tam giác PQR biết P = 70° R= 50°
3) Cho tam giác ABC vuông tại A , điểm K nằm giữa A và C . So sánh độ dài BK và BC
4) cho tam giác MNP vuông tại N . Trên tia đối của tia PN lấy điểm Q . So sánh độ dài MP và MQ
5) Cho tam giác ABC có ba góc nhọn AB < AC . Kẻ BD vuông góc với AC tại D , CD vuông góc với AB tại E . Gọi H là giao điểm của BC và CE . So sánh độ dài của HB và HC
B. Phần tự luận (6 điểm)
Cho tam giác ABC có hai đường cao AK và BH cắt nhau tại I, biết
∠ A = 60 o , ∠ B = 70 o
a. So sánh các cạnh của tam giác ABC
a. Hình vẽ ( 1 điểm)
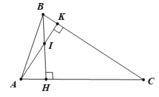
Vì ∠A = 60o,B = 70o nên ∠C = 180o - 60o - 70o = 50o ( 1 điểm)
Vì C < A < B ⇒ AB < BC < AC ( 1 điểm)
Đúng 0
Bình luận (0)
B. Phần tự luận (6 điểm)
Cho tam giác ABC có hai đường cao AK và BH cắt nhau tại I, biết
∠ A = 60 o , ∠ B = 70 o
a. So sánh các cạnh của tam giác ABC
a. Hình vẽ ( 1 điểm)
Vì ∠A = 60o,B = 70o nên ∠C = 180o - 60o - 70o = 50o ( 1 điểm)
Vì C < A < B ⇒ AB < BC < AC ( 1 điểm)
Đúng 0
Bình luận (0)
Bài 2: Cho tam giác ABC có góc A90 độ , lấy điểm M thuộc cạnh AB .a) So sánh AC và MC b) Chứng minh tam giác MBC là tam giác tùc) Chứng minh AC MC BCBài 3: Cho tam giác MNP có Góc N90 độ , trên tia đối của tia NP lấy điểm Q .a) So sánh MN và MP b) Chứng minh tam giác MPQlà tam giác tù.c) Chứng minh MNMPMQBài 4: Cho tam giác ABC có AB3 cm, AC4 cma) So sánh góc B với gócCb) Hạ AH vuông góc với BC tại H . So sánh góc BAH và góc CAHBài 5: Cho tam giác ABC có AB 5 cm, AC 3 cma) So sánh góc B với gó...
Đọc tiếp
Bài 2: Cho tam giác ABC có góc A>90 độ , lấy điểm M thuộc cạnh AB .
a) So sánh AC và MC
b) Chứng minh tam giác MBC là tam giác tù
c) Chứng minh AC <MC <BC
Bài 3: Cho tam giác MNP có Góc N>90 độ , trên tia đối của tia NP lấy điểm Q .
a) So sánh MN và MP
b) Chứng minh tam giác MPQlà tam giác tù.
c) Chứng minh MN<MP<MQ
Bài 4: Cho tam giác ABC có AB=3 cm, AC=4 cm
a) So sánh góc B với gócC
b) Hạ AH vuông góc với BC tại H . So sánh góc BAH và góc CAH
Bài 5: Cho tam giác ABC có AB = 5 cm, AC = 3 cm
a) So sánh góc B với góc C
b) So sánh hai góc ngoài tại các đỉnh B và C của tam giác ABC
Bài 6: Cho tam giác ABC vuông tại A có AC=2AB . Lấy điểm E trên cạnh AC sao cho
AB=AE . Trên tia đối của tia EB lấy điểm D sao cho EB=ED
a) Chứng minh tam giác ABE= tam giác CDE
b) So sánh góc ABE và góc CBE
B. Phần tự luận (6 điểm)
Cho tam giác ABC có hai đường cao AH, BK cắt nhau tại điểm M. Biết
∠ A = 55 o , ∠ B = 67 o
a. So sánh các cạnh của tam giác ABC
a. Hình vẽ ( 1 điểm)
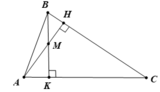
Vì ∠A = 55o, ∠B = 67o nên ∠C = 180o - 55o - 67o = 58o
Vì A < C < B ⇒ BC < AB < AC ( 1 điểm)
Đúng 0
Bình luận (0)