Đồ thị hàm số y = x 4 − 8 x 3 + 1 nghịch biến trên khoảng nào (khoảng lớn nhất)?
A. 0 ; 6
B. 6 ; + ∞
C. − ∞ ; 8
D. − ∞ ; 6
Cho hàm số y=f(x) xác định trên ℝ và có đồ thị của hàm số f’(x) và các khẳng định sau:
(1). Hàm số y=f(x) đồng biến trên khoảng 1 ; + ∞
(2). Hàm số y=f(x) nghịch biến trên khoảng - ∞ ; - 2
(3). Hàm số y=f(x) nghịch biến trên khoảng - 2 ; 1 .
(4). Hàm số y = f x 2 đồng biến trên khoảng - 1 ; 0
(5). Hàm số y = f x 2 nghịch biến trên khoảng (1;2)

Số khẳng định đúng là
A. 4
B. 3
C. 2
D. 5
Cho hàm số y= f(x) . Đồ thị hàm số y= f’(x) như hình bên. Hỏi hàm số y= g(x) = f(1-x2) nghịch biến trên khoảng nào trong các khoảng sau?
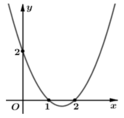
A. (1; 2)
B. (0; + ∞)
C. (-2; -1)
D. (-1; 1)
Cho hàm số f (x) Đồ thị hàm số y=f'(x) như hình vẽ bên. Hàm số g(x)=f(3-2x) nghịch biến trên khoảng nào trong các khoảng sau?
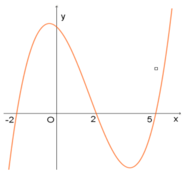
A.![]()
B.![]()
C.![]()
D.![]()
Cho hàm số y=f(x) có đồ thị f '(x) nhưu hình vẽ bên dưới
Hàm số y=f(3-2x) nghịch biến trên khoảng nào trong các khoảng sau?
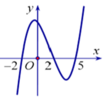
A. - 1 ; + ∞ .
B.(0;2)
C. - ∞ ; - 1 .
D.(1;3)
Cho hàm số y = f(x) có đồ thị f'(x) như hình vẽ bên dưới. Hàm số y = f(3-2x) nghịch biến trên khoảng nào trong các khoảng sau?
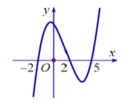
A. (1;+ ∞ )
B. (0;2)
C. (- ∞ ;-1)
D. (1;3)
Chọn C.
Dựa vào đồ thị hàm số f'(x) ta thấy
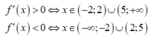
Xét hàm số y = f(3-2x) có y' = -2.f'(3-2x)
Hàm số y = f(3-2x) nghịch biến ![]()
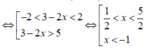
Vậy hàm số y = f(3-2x) nghịch biến trên các khoảng 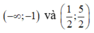
Cho hàm số y=f(x) có đạo hàm trên R thỏa mãn f(-1)= f(3)= 0 và đồ thị hàm số y=f' (x) có dạng như hình vẽ. Hàm số y= [ f ( x ) ] 2 nghịch biến trên khoảng nào trong các khoảng sau?
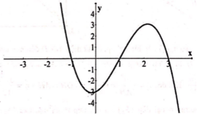
A. (-2;1).
B. (1;2).
C. (0;4).
D. (-2;2).
Cho hàm số y = f(x). Hàm số y = f'(x) có đồ thị như hình bên. Hàm số y = f ( 3 − x 2 ) nghịch biến trên khoảng nào?
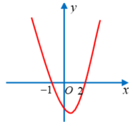
A. (0;2)
B. (-1;2)
C. (1;2)
D. (-2;-1)
Cho đồ thị hàm số y = f(x) có đồ thị như hình vẽ bên. Hàm số y = f(x) nghịch biến trên khoảng nào dưới đây?
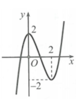
A. (0;+¥)
B. (0;2)
C. (-¥;2)
D. (-2;2)
Cho hàm số y=f(x) liên tục trên đoạn [-1;4] và có đồ thị hàm số y=f’(x) như hình bên. Hỏi hàm số g ( x ) = f x 2 + 1 nghịch biến trên khoảng nào trong các khoảng sau?
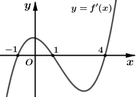
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
![]()
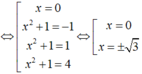
Các nghiệm trên đều là các nghiệm bội lẻ, do đó đều là cực trị của hàm số ![]()
Xét x = -1 ta có ![]()
từ đó ta có bảng xét dấu g’(x) như sau:
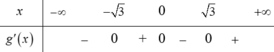
Dựa vào các đáp án ta thấy hàm số y = g(x) nghịch biến trên (0;1)
Chọn B