Tiếp theo câu 8. Chiết suất n của lăng kính có giá trị nào sau đây? (Tính với một chữ só thập phân).
A. 1,4
B. 1,5
C. 1,7
D. Khác A, B, C
Tiếp theo bài tập 5
Chiết suất n của lăng kính có giá trị nào sau đây? (Tính với một chữ só thập phân).
A. 1,4
B. 1,5
c. 1,7
D. Khác A, B, C
Ta thấy tia ló truyền đi sát mặt BC ⇒ góc tới mặt BC bằng góc giới hạn: r2 = igh
Và sin igh = 1/n
Mà 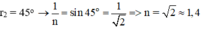
Đáp án: A
Cho tia sáng truyền tới lăng kính như Hình 28.9
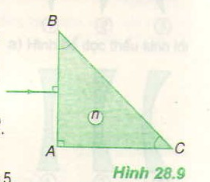
Bài 5: Tia ló truyền đi sát mặt BC. Góc lệch tạo bởi lăng kính có giá trị nào sau đây?
A. 0o.
B. 22,5o.
C. 45o.
D. 90o.
Bài 6: Chiết suất n của lăng kính có giá trị nào sau đây? (Tính tròn tới một chữ số thập phân)
A. 1,4.
B. 1,5.
C. 1,7.
D. Khác A, B, C.
Cho tia sáng truyền tới lăng kính như hình . Tia ló truyền đi đi sát mặt BC. Chiết suất n của lăng kính có giá trị nào sau đây? (Tính với một chữ só thập phân).

A. 1,4
B. 1,5
C. 1,7
D. Khác A, B, C
Cho tia sáng truyền tới lăng kính như hình vẽ. Tia ló truyền đi đi sát mặt BC. Chiết suất n của lăng kính có giá trị nào sau đây? (Tính tròn với 1 chữ số thập phân)
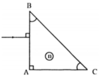
A.1,4
B.1,5
C.1,7
D. Khác A, B, C
Đáp án cần chọn là: A
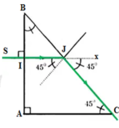
Ta có ΔABC vuông cân ⇒ B ^ = C ^ = 45 0
S I ⊥ A B ⇒ Tia SI truyền thẳng vào môi trường trong suốt ABC mà không bị khúc xạ
→ Góc tới ở mặt AB là i 1 = 0 và góc khúc xạ r 1 = 0
Góc tới mặt BC là: r 2 = 90 0 − B J I ^ = 90 0 − 45 0 = 45 0
Tia ló truyền sát mặt BC → Góc ló i 2 = 90 0
Áp dụng định luật khúc xạ ánh sáng ta có:
n . sin r 2 = sin i 2 ⇒ n = sin i 2 sin r 2 = sin 90 sin 45 = 1,4
Lăng kính với chiết quang A=30 độ. Chiết suất n=1,5. Một chùm tia sáng hẹp đơn sắc được chiếu vuông góc đến mặt trước của lăng kính. a) Tính góc lệch D b) Giữ chùm tia tới cố định, thay lăng kính bằng một lăng kính có cùng kích thước nhưng chiết suất n' khác n, xác định n' để tia ló đi sát mặt sau của lăng kính
Lăng kính có chiết suất n và góc chiết quang A = 30 0 . Một chùm tia sáng hẹp, đơn sắc được chiếu vuông góc đến mặt trước của lăng kính. Nếu chùm tia ló sát mặt sau của lăng kính thì n gần giá trị nào nhất sau đây?
A. 1,4.
B. 1,5.
C. 1,7.
D. 1,8.
Đáp án D
+ Vì chiếu vuông góc với mặt bên nên tia sáng truyền thẳng đến mặt bên thứ 2
® Góc tới với mặt bên thứ 2 là i = A = 30 0
+ CHùm tia ló ra sát mặt bên thứ 2 nên: nsin 30 0 = sin 90 0
® n = 2
® Gần 1,8 nhất
Một lăng kính có góc chiết quang là A = 8 ° . Chiếu một tia ánh sáng trắng vào mặt bên, gần sát góc chiết quang của lăng kính theo phương vuông góc với mặt phẳng phân giác của góc chiết quang A. Đặt màn quan sát sau lăng kính, song song với mặt phân giác của lăng kính và cách mặt phân giác này 1,5 m. Chiết suất của lăng kính đối với tia đỏ là 1,50 và đối với tia tím là 1,54. Độ rộng của vùng quang phổ liên tục trên màn quan sát là
A. 4,65 mm
B. 7,82 mm
C. 8,42 mm
D. 10,08 mm
Một lăng kính có góc chiết quang là A= 8 ° . Chiếu một tia ánh sáng trắng vào mặt bên, gần sát góc chiết quang của lăng kính theo phương vuông góc với mặt phẳng phân giác của góc chiết quang A. Đặt màn quan sát sau lăng kính, song song với mặt phân giác của lăng kính và cách mặt phân giác này 1,5 m. Chiết suất của lăng kính đối với tia đỏ là 1,50 và đối với tia tím là 1,54. Độ rộng của vùng quang phổ liên tục trên màn quan sát là
A. 7,82 mm
B. 10,08 mm
C. 8,42 mm
D. 4,65 mm
Một lăng kính thủy tinh có chiết suất n=1,6. Chiếu một tia sáng đơn sắc theo phương vuông góc với mặt bên của lăng kính. Tia sáng phản xạ toàn phần ở mặt bên của lăng kính. Tính giá trị nhỏ nhất của góc chiết quang A.
A. 51,3 0
B. 32 0
C. 38,7 0
D. 58 0
Đáp án cần chọn là: C
+ Ta có, chiếu tia sáng đơn sắc theo phương vuông góc với mặt bên của lăng kính
⇒ i 1 = 0 ⇒ r 1 = 0 0
+ Góc chiết quang A = r 1 + r 2 = 0 0 + r 2 ⇒ A = r 2
Vì xảy ra phản xạ toàn phần nên ta suy ra r 2 ≥ i g h ⇒ A ≥ i g h
+ Ta có có giới hạn phản xạ toàn phần khi ánh sáng truyền từ lăng kính ra môi trường không khí bên ngoài
sin i g h = n k k n l k = 1 n = 1 1,6
⇒ i g h = 38,7 0
Ta suy ra:
A ≥ i g h = 38,7 0
⇒ A min = 38,7 0