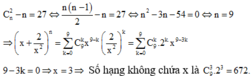Với n là số nguyên dương thỏa mãn C n 1 + C n 2 = 55 , số hạng không chứa x trong khai triển của biểu thức x 3 + 2 x 2 n bằng
A. 322560
B. 3360
C. 80640
D. 13440
Với n là số nguyên dương thỏa mãn C n 1 + C n 2 = 55 số hạng không chứa x trong khai triển của biểu thức x 3 + 2 x 2 n bằng:
A. 322560
B. 3360
C. 80640
D. 13440
Với n là số nguyên dương thỏa mãn C n 1 + C n 2 = 55 , số hạng không chứa x trong khai triển của biểu thức x 3 + 2 x 2 n bằng:
A. 322560
B. 3360
C. 80640
D. 13440
Với n là số nguyên dương thỏa mãn C n 1 + C n 2 = 55 số hạng không chứa x trong khai triển của biểu thức x 3 + 2 x 2 n bằng
A. 322560
B. 3360
C. 80640
D. 13440
Với n là số nguyên dương thỏa mãn C n 1 + C n 2 = 55 , số hạng không chứa x trong khai triển của biểu thức x 3 + 2 x 2 n bằng
A. 322560
B. 3360
C. 80640
D. 13440
Với n là số nguyên dương thỏa mãn C n 1 + C n 2 = 55 , số hạng không chứa x trong khai triển của biểu thức x 3 + 2 x 2 n bằng
A. 322560
B. 3360
C. 80640
D. 13440
C n 1 + C n 2 = 55
⇔ n ! n - 1 ! . 1 ! + n ! n - 2 ! . 2 ! = 55 ⇔ n + n . n - 1 2 = 55 ⇔ 2 n + n 2 - n = 110 ⇔ n = 10 n = - 11 l
x 3 + 2 x 2 n
= ∑ k = 0 10 . C 10 k . x 3 10 - k . 2 x 2 k = ∑ k = 0 10 . C 10 k . 2 k . x 30 - 3 k - 2 k
Số hạng không chứa x trong khai triển ⇒ tìm hệ số của số hạng chứa x 0 trong khai triển
⇒ x 30 - 3 k - 2 k = x 0 ⇔ k = 6
Vậy số hạng cần tính là C 10 6 . 2 6 = 13440
Đáp án cần chọn là D
Với n là số nguyên dương thỏa mãn C n 1 + C n 2 = 55 , số hạng không chứa x trong khai triển của biểu thức x 2 + 2 x 2 n bằng.
A. 322560
B. 3360
C. 80640
D. 13440
Đáp án D.
Ta có
C n 1 + C n 2 = 55 ⇔ n ! 1 ! n − 1 ! + n ! 2 ! n − 2 ! = 55 ⇔ n + 1 2 n n − 1 = 55 ⇔ n = 10 n = − 11 l
Khi đó
x 3 + 2 x 2 n = x 3 + 2 x 2 10 = ∑ n = 0 10 C 10 n x 3 n 2 x 2 10 − n = ∑ n = 0 10 C 10 n 2 10 − n x 5 n − 20
Số hạng không chưa x khi 5 n − 20 = 0 ⇔ n = 4 ⇒ n = 4 ⇒ số hạng không chứa x là C 10 4 .2 10 − 4 = 13440.
Với n là số nguyên dương thỏa mãn C n 1 + C n 2 = 55 . Hệ số của số hạng chứa trong khai triển của biểu thức x 3 + 2 x 2 n bằng
A. 8064
B. 3360
C. 8440
D. 6840
Với n là số nguyên dương thỏa mãn C n 1 + C n 2 = 55 . Hệ số của số hạng chứa x 5 trong khai triển của biểu thức x 3 + 2 x 2 n bằng
A. 8064
B. 3360
C. 8440
D. 6840
Với số nguyên dương n thỏa mãn C n 2 − n = 27 , trong khai triển x + 2 x 2 n số hạng không chứa x là:
A. 84
B. 8
C. 5376
D. 672
Đáp án D.
Phương pháp
Sử dụng công thức C n k = n ! k ! n − k ! tìm n.
Sử dụng khai triển nhị thức Newton
a + b n = ∑ k = 0 n C n k . a n − k . b k
Cách giải