Tìm điều kiện cần và đủ của a, b, c để phương trình asinx+bcosx=c có nghiệm
![]()
![]()
![]()
![]()
Tìm điều kiện cần và đủ của a, b, c để phương trình a sin x + b cos x = c có nghiệm?
A. a 2 + b 2 > c 2
B. a 2 + b 2 ≤ c 2
C. a 2 + b 2 = c 2
D. a 2 + b 2 ≥ c 2
Chọn D.
Phương pháp:
Phương trình thuần nhất đối với sin và cos, dạng
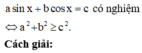
Phương trình thuần nhất đối với sin và cos, dạng
![]()
Tìm điều kiện cần và đủ của a, b, c để phương trình a . sin x + b . cos x = c có nghiệm?
![]()
![]()
![]()
![]()
Xét phương trình bậc hai az2+bz+c=0 trên tập C a ≠ 0 , a , b , c ∈ R . Tìm điều kiện cần và đủ để phương trình có hai nghiệm z1 và z2 là số phức liên hợp với nhau.
![]()
![]()
![]()
![]()
Nêu cách giải phương trình lượng giác cơ bản , cách giải phương trình a sin x + b cos x = c .
a) Cách giải các phương trình lượng giác cơ bản:
+ Phương trình sin x = a.
Nếu |a| > 1 ⇒ phương trình vô nghiệm.
Nếu |a| ≤ 1 ⇒ tìm một cung α sao cho sin α = a.
Khi đó phương trình trở thành sin x = sin α
⇒ Phương trình có nghiệm: 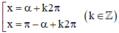
+ Phương trình cos x = a.
Nếu |a| > 1 ⇒ phương trình vô nghiệm.
Nếu |a| ≤ 1 ⇒ tìm một cung α sao cho cos α = a.
Khi đó phương trình trở thành cos x = cos α.
⇒ Phương trình có nghiệm: x = ±α + k2π (k ∈ Z).
+ Phương trình tan x = a.
Tìm một cung α sao cho tan α = a.
Khi đó phương trình trở thành tan x = tan α.
⇒ Phương trình có nghiệm x = α + kπ (k ∈ Z).
+ Phương trình cot x = a
Tìm một cung α sao cho cot α = a.
Khi đó phương trình trở thành cot x = cot α.
⇒ Phương trình có nghiệm x = α + kπ (k ∈ Z).
b) Cách giải phương trình a.sin x + b.cos x = c.
+ Nếu a = 0 hoặc b = 0 ⇒ Phương trình lượng giác cơ bản .
+ a ≠ 0 và b ≠ 0. Chia cả hai vế của phương trình cho  ta được:
ta được:

Ta giải phương trình trên như phương trình lượng giác cơ bản.
cho phương trình (m - 1.x+ m =0) a) Tìm điều kiện của m để phương trình trên là phương trình bậc nhất một ẩn. b)Tìm điều kiện của m để phương trình trên có nghiệm x = -5 c)Tìm điều kiện của m để phương trình trên vô nghiệm.
Biết điều kiện cần và đủ của m để phương trình log 2 1 2 x - 2 2 + 4 m - 5 log 1 2 1 x - 2 - 8 m - 4 = 0 . Có nghiệm thuộc 5 4 ; 4 là m ∈ a ; b . Tính T=a+b
A. 10 3
B. 4
C. -4
D. - 10 3
Tìm điều kiện cần và đủ về các số thực m,n để phương trình z 4 + m z 2 + n = 0 không có nghiệm thực
![]()
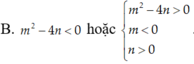
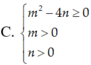

Để hệ phương trình x + y = S x . y = P có nghiệm, điều kiện cần và đủ là:
A. S 2 − P < 0
B. S 2 − P ≥ 0
C. S 2 − 4 P < 0
D. S 2 − P ≥ 0
- Ta có: x, y là nghiệm phương trình X 2 - S X + P = 0
- Hệ phương trình có nghiệm khi ∆ = S 2 - 4 P ≥ 0
Đáp án cần chọn là: D
Để hệ phương trình x + y = S x y = P có nghiệm, điều kiện cần và đủ là:
A. S 2 – P < 0
B. S 2 – P ≥ 0
C. S 2 – 4 P < 0
D. S 2 – 4 P ≥ 0