Chọn C

Chọn A

Theo giả thiết ta có :

y = x q ;     z = x q 2 x + 3 z = 2 2 y ⇒ x + 3 x q 2 = 4 x q ⇒ x 3 q 2 − 4 q + 1 = 0 ⇔ x = 0 3 q 2 − 4 q + 1 = 0 .

Nếu x = 0 ⇒ y = z = 0 ⇒  công sai của cấp số cộng: x ; 2y ;  3z bằng 0 (vô lí).

nếu

3 q 2 − 4 q + 1 = 0 ⇔ q = 1 q = 1 3 ⇔ q = 1 3    q = 1 .

Đáp án D

Chọn D

Đáp án B

Vì x , y , z > 0  theo thứ tự lập thành 1 CSN nên  z = q y = q 2 x .

Vì log a x , log a y , log a 3 z  theo thứ tự lập thành cấp số cộng nên  2 log a y = log a x + log a 3 z

⇔ 4 log a y = log a x + 3 log a z ⇔ 4 log a q x = log a x + 3 log a q 2 x ⇔ log a q 4 x 4 = log a x q 3 x 3

⇔ q 4 x 4 = q 6 x 4 ⇒ q = 1 ⇒ x = y = z ⇒ P = 1959 + 2019 + 60 = 4038

Đáp án D

Ta có y 2 = x z và

log a x + log a 3 = 2 log 2 y ⇔ log a x + log a z 3 = log a y 4 ⇒ x z 3 = y 4 − x 2 z 2 ⇒ x = z ⇒ x = y = z

Theo giả thiết ta có  x + 6 y + 8 x + y = 2 5 x + 2 y x − 1 x − 3 y = y + 2 2

⇔ x = 3 y 3 y − 1 3 y − 3 y = y + 2 2 ⇔ x = 3 y 0 = y + 2 2 ⇔ x = − 6 y = − 2 .

Suy ra  x 2 + y 2 = 40.

Chọn đáp án A.

Chọn A

+ Ba số x + 6 y ,5 x + 2 y ,8 x + y  lập thành cấp số cộng nên

x + 6 y + 8 x + y = 2 5 x + 2 y ⇔ 9 x + ​ 7 y =    10 x + ​  4 y   ⇔ x = 3 y

+ Ba số x + 5 3 , y − 1,2 x − 3 y  lập thành cấp số nhân nên x + 5 3 2 x − 3 y = y − 1 2 .

Thay x= 3y vào ta được :

3 y + 5 3 2.3 y − 3 y = y − 1 2 ⇔ 3 y + 5 3 .3 y =    y 2 − 2 y + ​    1 ⇔ 9 y 2 + ​ 5 y −    y 2 + ​ 2 y −     1 = 0

⇔ 8 y 2 + 7 y − 1 = 0 ⇔ y = − 1 hoặc  y = 1 8 .

Với y= -1 thì x= - 3; với y = 1 8  thì x = 3 8 .

Ta có hệ phương trình:

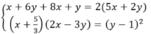
Từ đó ta suy ra

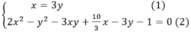
Thế (1) vào (2) ta được: 8y2+7y-1=0⇒y=-1 hoặc y=1/8

Do y < 0 , ta được y = -1, x = -3

Đáp án B