Chọn C

Đáp án D.

Ta có:

P T ⇔ m 9 4 x − 2 m + 1 6 4 x + m ≤ 0 ⇔ m 3 2 2 x − 2 m + 1 3 2 x + m ≤ 0

Đặt t = 3 2 x ;  do x ∈ 0 ; 1 ⇒ t ∈ 1 ; 3 2 .  Khi đó PT trở thành: m t 2 − 2 m + 1 t + m ≤ 0 ⇔ m t 2 − 2 t + 1 ≤ t

Rõ ràng t = 1 là nghiệm của BPT đã cho.

Với t ∈ 1 ; 3 2 ⇒ m ≤ t t − 1 2 = f t ,  xét f x  với t ∈ 1 ; 3 2  ta có:

f ' t = t − 1 − 2 t t − 1 3 = − t − 1 t − 1 2 < 0 ∀ t ∈ 1 ; 3 2

do đó f t   nghịch biến trên 1 ; 2 3 .

Do đó BPT nghiệm đúng vơi ∀ t ∈ 1 ; 3 2 ⇔ m ≤ M i n 1 ; 3 2 f t = f 3 2 = 6

Vậy có 6 giá trị nguyên dương của m thỏa mãn.

Đáp án D.

Ta có:

P T ⇔ m 9 4 x - 2 m + 1 6 4 x + m ≤ 0

⇔ m 3 2 2 x - 2 m + 1 3 2 x + m ≤ 0

Đ ặ t   t = 3 2 x ;   d o   x ∈ 0 ; 1 ⇒ t ∈ 1 ; 3 2 .

Khi đó PT trở thành:

  m t 2 - 2 m + 1 t + m ≤ 0 ⇔ m t 2 - 2 t + 1 ≤ t

Rõ ràng t =1 là nghiệm của BPT đã cho.

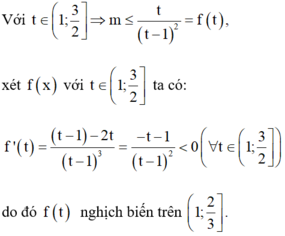
D o   đ ó   B P T   n g h i ệ m   đ ú n g   v ớ i   ∀ t ∈ 1 ; 3 2

⇔ m ≤ M i n 1 ; 3 2 f t = f 3 2 = 6 .

Vậy có 6 giá trị nguyên dương của m thỏa mãn.

Chọn B

Có 

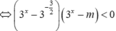
+) Nếu m ≤ 0 bất phương trình tương đương với  chứa vô số các số nguyên (loại);

+) Nếu 0 < m < 3 - 3 2  không có số nguyên m nào cả (loại).

+) Nếu m > 3 - 3 2 bất phương trình tương đương với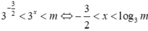 

Tập nghiệm là 

Vì S chứa đúng 10 số nguyên do đó  ⇒ m ∈ 3 8 + 1 , . . . , 3 9 Có tất cả  3 9 - 3 8 số nguyên thoả mãn.

Chọn đáp án D.

Chọn A