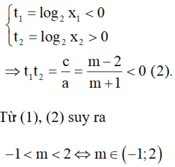Tập hợp các giá trị m để phương trình
e
x
m
-
2019
có nghiệm thực là
Đọc tiếp
Tập hợp các giá trị m để phương trình
e x = m - 2019 có nghiệm thực là
Những câu hỏi liên quan
Tập hợp các số thực m để phương trình
ln
x
2
-
m
x
-
2019
ln
x
có nghiệm duy nhất là A.
∅
B.
-
1
C.
0
D.
ℝ...
Đọc tiếp
Tập hợp các số thực m để phương trình ln x 2 - m x - 2019 = ln x có nghiệm duy nhất là
A. ∅
B. - 1
C. 0
D. ℝ
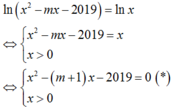
Nhận thấy phương trình (*) có a c < 0 ⇒ * có 2 nghiệm phân biệt, do đó ∀ m ∈ ℝ phương trình (*) luôn có 1 nghiệm thỏa mãn x > 0 .
Chọn D.
Đúng 0
Bình luận (0)
Tập hợp tất cả các giá trị thực của m để phương trình
l
o
g
2
(
x
+
m
+
1
)
l
o
g
2
(
m
2
-
4
x
+
4
m
x
)
có đúng một nghiệm thực là A.
-...
Đọc tiếp
Tập hợp tất cả các giá trị thực của m để phương trình l o g 2 ( x + m + 1 ) = l o g 2 ( m 2 - 4 x + 4 m x ) có đúng một nghiệm thực là
A. - 2 3 3 ; 2 3 3
B. - 2 3 3 ; 2 3 3 ∪ 4 + 2 2
C. [ - 2 3 3 ; 2 3 3 ) ∪ 4 ± 2 2
D. - 2 3 3 ; 2 3 3 ∪ 4 ± 2 2
Tập hợp các giá trị thực của m để phương trình
cos
2
x
+
2
m
.
sin
x
.
cos
x
5
có nghiệm là?
Đọc tiếp
Tập hợp các giá trị thực của m để phương trình cos 2 x + 2 m . sin x . cos x = 5 có nghiệm là?
Cho phương trình
sin
x
+
m
2
3
+
sin
2
x
-
m
2...
Đọc tiếp
Cho phương trình sin x + m 2 3 + sin 2 x - m 2 3 = 2 sin x - m 2 3 . Gọi S = [a;b] là tập hợp tất cả các giá trị thực của tham số m để phương trình trên có nghiệm thực. Tìm giá trị của P = a 2 + b 2
A. P = 162 49
B. P = 49 162
C. P = 4
D. P = 2
Gọi S là tập hợp các giá trị thực của tham số m để phương trình
4
x
-
m
.
2
x
+
2
m
+
1
0
có nghiệm. Tập RS có bao nhiêu giá trị nguyên? A.1 B.4 C.9 D.7
Đọc tiếp
Gọi S là tập hợp các giá trị thực của tham số m để phương trình 4 x - m . 2 x + 2 m + 1 = 0 có nghiệm. Tập R\S có bao nhiêu giá trị nguyên?
A.1
B.4
C.9
D.7
Gọi S là tập hợp các giá trị thực của tham số m để phương trình 4 x – m . 2 x + 2 m + 1 = 0 có nghiệm. Tập R\S có bao nhiêu giá trị nguyên
A. 1
B. 4
C. 9
D. 7
Cho S là tập hợp các giá trị thực của tham số m để phương trình
2
−
x
+
1
−
x
m
+
x
−
x
2
có hai nghiệm phân biệt. Tổng các số nguyên trong S bằng A. 11 B. 0 C. 5 D. 6
Đọc tiếp
Cho S là tập hợp các giá trị thực của tham số m để phương trình 2 − x + 1 − x = m + x − x 2 có hai nghiệm phân biệt. Tổng các số nguyên trong S bằng
A. 11
B. 0
C. 5
D. 6
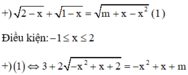
Đặt − x 2 + x = t ;
f x = − x 2 + x ; f ' x = − 2 x + 1
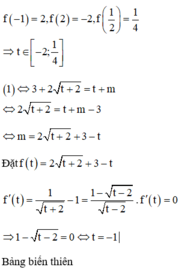
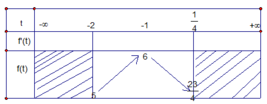
Chọn A
Đúng 0
Bình luận (0)
Cho S là tập hợp các giá trị thực của tham số m để phương trình
2
-
x
+
1
-
x
m
+
x
-
x
2
có hai nghiệm phân biệt. Tổng các số nguyên trong S bằng A. 11. B. 0. C. 5. D. 6.
Đọc tiếp
Cho S là tập hợp các giá trị thực của tham số m để phương trình 2 - x + 1 - x = m + x - x 2 có hai nghiệm phân biệt. Tổng các số nguyên trong S bằng
A. 11.
B. 0.
C. 5.
D. 6.
Đáp án A
+)
(
)
Điều kiện:
+)
Đặt:
Đặt
.
Bảng biến thiên
+) 
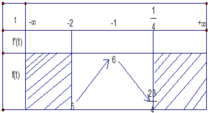
Để phương trình có hai nghiệm phân biệt
Do đó để phương trình có hai nghiệm phân biệt thì phương trình
có nghiệm
Từ bảng biến thiên
.
Đúng 0
Bình luận (0)
Cho phương trình
m
+
1
log
2
2
x
+
2
log
2
x
+
m
-
2
0
. Tìm tập hợp tất cả các giá trị của tham số thực m để phương trình đã cho có hai nghiệm thực x1, x2 thỏa 0 x1 1 x2 A. ...
Đọc tiếp
Cho phương trình m + 1 log 2 2 x + 2 log 2 x + m - 2 = 0 . Tìm tập hợp tất cả các giá trị của tham số thực m để phương trình đã cho có hai nghiệm thực x1, x2 thỏa 0 < x1 < 1 < x2
A. 2 ; + ∞
B. - 1 ; 2
C. - ∞ ; - 1
D. - ∞ ; - 1 ∪ 2 ; + ∞
Đáp án B.
Đặt t = log2 x,
khi đó m + 1 log 2 2 x + 2 log 2 x + m - 2 = 0
⇔ m + 1 t 2 + 2 t + m - 2 = 0 (*).
Để phương trình (*) có hai nghiệm phân biệt
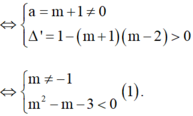
Khi đó gọi x1, x2 lần lượt hai nghiệm của phương trình (*).
Vì 0 < x1 < 1 < x2 suy ra
Đúng 0
Bình luận (0)