Biết rằng có duy nhất 1 cặp số thực (x;y) thỏa mãn (x+y)+(x-y)i5+3i . Tính Sx+2y. A. . B. . C.. D. .
Đọc tiếp
Biết rằng có duy nhất 1 cặp số thực (x;y) thỏa mãn (x+y)+(x-y)i=5+3i . Tính S=x+2y.
A. 
.
B. 
.
C.
.
D. 
.
Những câu hỏi liên quan
Có bao nhiêu số thực m để tôn tại duy nhất cặp số thực (x;y) thỏa mãn đồng thời
log
x
2
+
y
2
+
2
4
x
+
4
y
+
m
2
-...
Đọc tiếp
Có bao nhiêu số thực m để tôn tại duy nhất cặp số thực (x;y) thỏa mãn đồng thời log x 2 + y 2 + 2 4 x + 4 y + m 2 - m - 5 ≥ 1 và x 2 + y 2 + 2 x - 4 x + 1 = 0 .
A. 2.
B. 6.
C. 4.
D. 0.
Biết rằng trong tất cả các cặp (x;y) thỏa mãn
log
2
x
2
+
y
2
+
2
≤
log
2
x
+
y
-
1
chỉ có duy nhất một cặp (x;y) thỏa mãn 3x+4y-m0....
Đọc tiếp
Biết rằng trong tất cả các cặp (x;y) thỏa mãn log 2 x 2 + y 2 + 2 ≤ log 2 x + y - 1 chỉ có duy nhất một cặp (x;y) thỏa mãn 3x+4y-m=0. Khi đó hãy tính tổng tất cả các giá trị m tìm được.
A. 20
B. 28
C. 46
D. 14
Biết rằng trong tất cả các cặp (x; y) thỏa mãn:
log
2
x
2
+
y
2
+
2
≤
2
+
log
2
x
+
y
-
1
. Chỉ có duy nhất một cặp (x;...
Đọc tiếp
Biết rằng trong tất cả các cặp (x; y) thỏa mãn: log 2 x 2 + y 2 + 2 ≤ 2 + log 2 x + y - 1 . Chỉ có duy nhất một cặp (x; y) thỏa mãn: 3x + 4y - m = 0 . Khi đó hãy tính tổng tất cả các giá trị m tìm được?
A. 20
B. 46
C. 28
D. 14
Biết rằng trong tất cả các cặp (x; y) thỏa mãn:
log
2
x
2
+
y
2
+
2
≤
log
2
x
+
y
-
1...
Đọc tiếp
Biết rằng trong tất cả các cặp (x; y) thỏa mãn: log 2 x 2 + y 2 + 2 ≤ log 2 x + y - 1 . Chỉ có duy nhất một cặp (x; y) thỏa mãn: 3x + 4y - m = 0 . Khi đó hãy tính tổng tất cả các giá trị m tìm được?
A. 20
B. 46
C. 28
D. 14
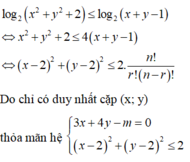
nên đường thẳng 3x + 4y - m = 0 là tiếp tuyến của đường tròn (x – 2)2 + (y – 2)2 = 2.
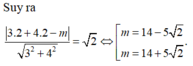
Chọn C.
Đúng 0
Bình luận (0)
Chứng minh rằng tồn tại duy nhất cặp số (x; y) thoả mãn:\(x^2-2y^2=1\)(với x, y là các số nguyên tố). Tìm cặp số (x; y) đó
\(Giải.\)
\(x^2-2y^2=1\Leftrightarrow x^2-1=2y^2\Leftrightarrow\left(x+1\right)\left(x-1\right)=2y^2\left(chẵn\right)\)
Dễ thấy: x+1-(x-1)=2 nên 2 số trên cùng chẵn hoặc cùng lẻ=> 2 số trên cùng chẵn
=> 2y2 chia hết cho 4=>y2 chia hết cho 2
=> y chẵn =>y=2=>x2-8=1=>x=3 (thỏa mãn)
Vậy chỉ có duy nhất 1 cặp: (x,y)=(3;2) thỏa mãn
Đúng 0
Bình luận (0)
Dễ thấy: x+1-(x-1)=2 nên 2 số trên cùng chẵn hoặc cùng lẻ=> 2 số trên cùng chẵn
=> 2y2 chia hết cho 4=>y2 chia hết cho 2
=> y chẵn =>y=2=>x2-8=1=>x=3 (thỏa mãn)
Vậy chỉ có duy nhất 1 cặp: (x,y)=(3;2) thỏa mãn
Đúng 0
Bình luận (0)
Biết rằng phương trình
2
+
5
x
+
1
8
5
-
2
2
x
-
1
có nghiệm duy nhất dạng
log...
Đọc tiếp
Biết rằng phương trình 2 + 5 x + 1 = 8 5 - 2 2 x - 1 có nghiệm duy nhất dạng log 2 + 5 a , với a là số thực dương. Mệnh đề nào dưới đây là đúng?
A. 0 < a < 4/5
B. 5 < a < 9
C. 4/5 < a < 12/5
D. 3 < a < 7/2
Chọn C.
Ta có: 
nên phương trình 
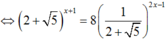
Do đó a = 2.
Đúng 0
Bình luận (0)
Trong tất cả các cặp số (x,y) thỏa mãn
log
x
2
+
y
2
+
3
2
x
+
2
y
+
5
≥
1
, giá trị thực của m để tồn tại duy nhất cặp (x,y) sao cho...
Đọc tiếp
Trong tất cả các cặp số (x,y) thỏa mãn log x 2 + y 2 + 3 2 x + 2 y + 5 ≥ 1 , giá trị thực của m để tồn tại duy nhất cặp (x,y) sao cho x 2 + y 2 + 4 x + 6 y + 13 - m = 0 thuộc tập nào sau đây?
A. [8;10]
B. [5;7]
C. [1;4]
D. [-3;0]
Đáp án A
Ta có, giả thiết log x 2 + y 2 + 3 2 x + 2 y + 5 ≥ x 2 + y 2 + 3 ≤ 2 x + 2 y + 5 ⇔ x - 1 2 + y - 1 2 ≤ 4 là miền trong đường tròn tâm I(1;1) bán kính R 1 = 2
Và x 2 + y 2 + 4 x + 6 y + 13 - m = 0 ⇔ x + 2 2 + y + 3 2 = m là đường tròn tâm I(-2;-3); R 2 = m
Khi đó, yêu cầu bài toán ⇔ R 1 + R 2 = I 1 I 2 ⇔ m + 2 = 5 ⇔ m = 9
Đúng 0
Bình luận (0)
Trong tất cả các cặp số (x,y) thỏa mãn
log
x
2
+
y
2
+
3
(
2
x
+
2
y
+
5
)
≥
1
giá trị thực của m để tồn tại duy nhất cặp (x,y) sao cho x2 + y2 + 4x + 6y + 13 - m 0 thuộc tập nào sau đây?
Đọc tiếp
Trong tất cả các cặp số (x,y) thỏa mãn log x 2 + y 2 + 3 ( 2 x + 2 y + 5 ) ≥ 1 giá trị thực của m để tồn tại duy nhất cặp (x,y) sao cho x2 + y2 + 4x + 6y + 13 - m = 0 thuộc tập nào sau đây?
Đáp án A
Ta có, giả thiết
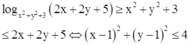
là miền trong đường tròn tâm I(1;1) bán kính R1 = 2
Và
Đúng 0
Bình luận (0)
Biết rằng phương trình
log
2
2
x
-
1
+
m
1
+
log
3
m
+
4
-
4
x
2
-...
Đọc tiếp
Biết rằng phương trình log 2 2 x - 1 + m = 1 + log 3 m + 4 - 4 x 2 - 1 có nghiệm thực duy nhất. Mệnh đề nào dưới đây đúng?
A. m∈(0;1).
B. m∈(1;3).
C. m∈(3;6).
D. m∈(6;9).
