Cho i là đơn vị ảo. Nghiệm của phương trình 3z+i-1=(i+2)/(i-2) là
A.![]()
B.![]()
C.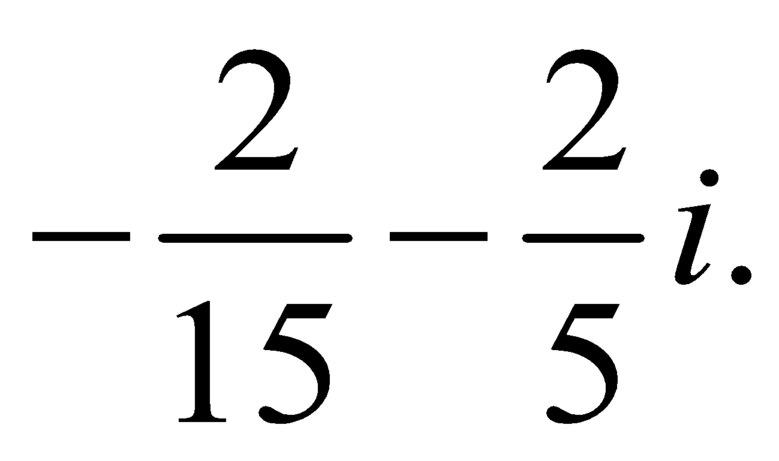
D.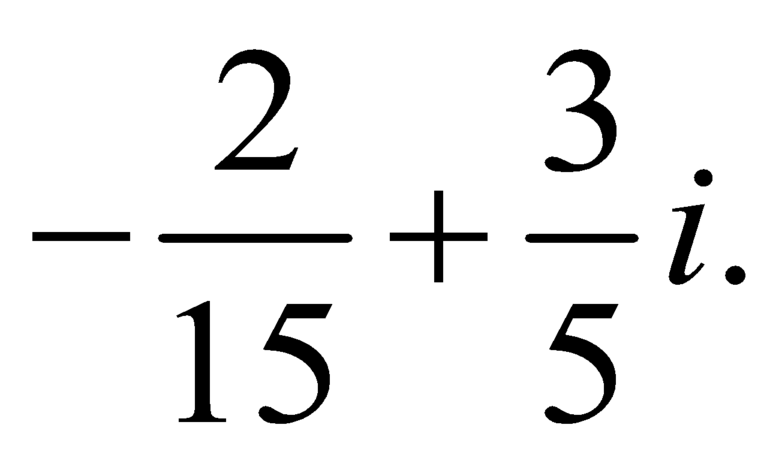
Cho i là đơn vị ảo. Tập hợp các điểm biểu diễn hình học số phức thỏa mãn z − i + 1 = z + i − 2 là đường thẳng có phương trình
A. 2 x − 3 y + 1 = 0
B. 6 x − 4 y − 3 = 0
C. 2 x − 3 y − 1 = 0
D. 4 x − 6 y + 3 = 0
Cho i là đơn vị ảo. Tập hợp các điểm biểu diễn hình học số phức thỏa mãn z - i + 1 = z + i - 2 là đường thẳng có phương trình
A. 2 x - 3 y - 1 = 0
B. 6 x - 4 y - 3 = 0
C. 2 x - 3 y + 1 = 0
D. 4 x - 6 y + 3 = 0
Cho i là đơn vị ảo. Tập hợp các điểm biểu diễn hình học số phức thỏa mãn |z-1+1| = |z+i-2| là đường thẳng có phương trình
![]()
![]()
![]()
![]()
Cho i là đơn vị ảo. Tập hợp các điểm biểu diễn hình học số phức thỏa mãn z - + 1 = z + i - 2 là đường thẳng có phương trình
![]()
![]()
![]()
![]()
Trong các khẳng định sau đây, khẳng định nào sai?
A:
ii là số phức thỏa mãn i^2=-1i2=−1.
B:
Số phức 2-9i2−9i có phần thực là 2 và phần ảo là -9−9.
C:
Số phức 2-i2−i có phần thực là 2 và phần ảo là 11.
D:
Phương trình x^2+1 = 0x2+1=0 có hai nghiệm trên tập số phức \mathbb{C}C là ii và -i−i.
Cho hai số thực a và b thỏa mãn: 1 + i z + 2 − i z ¯ = 13 + 2 i với i là đơn vị ảo
A. a = − 3 , b = 2
B. a = − 3 , b = − 2
C. a = 3 , b = − 2
D. a = 3 , b = 2
Cho phương trình z 3 + a z 2 + b z + c = 0 Nếu z=1-i và z=1 là 2 nghiệm của phương trình thì a - b - c bằng
A. 2
B. 3
C. 5
D. 6
Tìm các số thực a và b thoả mãn a+(b-i)i=1+3i với i là đơn vị ảo.
A.a = -2, b = 3
B. a = 1, b = 3
C. a = 2, b = 4
D. a = 0, b = 3
Tìm các số thực a và b thoả mãn a+(b-i)i=1+3i với i là đơn vị ảo
A.![]() .
.
B.![]() .
.
C.![]() .
.
D.![]() .
.