Trong không gian Oxyz, cho tứ diện ABCD có A ( 1 ; 0 ; 2 ) , B ( - 2 ; 1 ; 3 ) , C ( 3 ; 2 ; 4 ) , D ( 6 ; 9 ; - 5 ) . Tìm tọa độ trọng tâm G của tứ diện ABCD
A. G - 9 ; 18 4 ; - 30
B. G(8;12;4)
C. G 3 ; 3 ; 14 4
D. G(2;3;1)
Những câu hỏi liên quan
Trong không gian tọa độ Oxyz, cho tứ diện ABCD có A(1;0;0), B(0;1;0), C(0;0;1), D(-2;1;-1). Thể tích của tứ diện ABCD bằng A. 1 B. 2 C.
1
2
D.
1
3
Đọc tiếp
Trong không gian tọa độ Oxyz, cho tứ diện ABCD có A(1;0;0), B(0;1;0), C(0;0;1), D(-2;1;-1). Thể tích của tứ diện ABCD bằng
A. 1
B. 2
C. 1 2
D. 1 3
Chọn đáp án C.
Ta có
Áp dụng công thức ta có:
V A B C D = 1 6 A B ⇀ . A C ⇀ . A D ⇀ = 1 2
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho tứ diện ABCD có
A
(
1
;
0
;
2
)
,
B
(
-
2
;
1
;
3
)
,
C
(
3
;
2
;
4
)
,
D
(
6
;
9
;
-
5
)
.
Tìm tọa độ trọng tâm G của tứ diện ABCD A.
G
-
9...
Đọc tiếp
Trong không gian Oxyz, cho tứ diện ABCD có A ( 1 ; 0 ; 2 ) , B ( - 2 ; 1 ; 3 ) , C ( 3 ; 2 ; 4 ) , D ( 6 ; 9 ; - 5 ) . Tìm tọa độ trọng tâm G của tứ diện ABCD
A. G - 9 ; 18 4 ; - 30
B. G(8;12;4)
C. G 3 ; 3 ; 14 4
D. G(2;3;1)
Chọn D.
Gọi G(a,b,c) là trọng tâm của tứ diện, ta có:
Đúng 0
Bình luận (0)
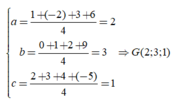
Trong không gian Oxyz, cho tứ diện ABCD với A(-1;-2;4), B(-4;-2;0), C(3;-2;1), D(1;1;1). Độ dài đường cao của tứ diện ABCD kẻ từ đỉnh D bằng
A. 3
B. 1
C. 2
D. 1 2
Trong không gian Oxyz. Cho tứ diện đều ABCD có A(0;1;2) và hình chiếu vuông góc của A trên mặt phẳng (BCD) là H (4; -3;-2). Tọa độ tâm I của mặt cầu ngoại tiếp tứ diện ABCD.
A. I(3; -2;-1).
B. I(2;-1;0).
C. I(3; -2;1).
D. I(-3; -2;1).
Trong không gian tọa độ Oxyz, cho tứ diện ABCD với A(-1;-2;4), B(-4;-2;0), C(3;-2;1) và D(1;1;1) . Độ cao của tứ diện kẻ từ D bằng
A. 3.
B. 1.
C. 2.
D. 0,5
Trong không gian Oxyz, cho tứ diện ABCD với A(1;2;1), B(2;1;3), C(3;2;2), D(1;1;1). Độ dài chiều cao DH của tứ diện bằng A.
3
14
14
B.
14
14
C.
4
14
7
D.
3...
Đọc tiếp
Trong không gian Oxyz, cho tứ diện ABCD với A(1;2;1), B(2;1;3), C(3;2;2), D(1;1;1). Độ dài chiều cao DH của tứ diện bằng
A. 3 14 14
B. 14 14
C. 4 14 7
D. 3 14 7
Trong không gian với hệ trục tọa độ Oxyz, cho tứ diện ABCD với
A
0
;
1
;
1
,
B
0
;
2
;
1
,
C
−
1
;
0
;
2
,...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho tứ diện ABCD với A 0 ; 1 ; 1 , B 0 ; 2 ; 1 , C − 1 ; 0 ; 2 , D − 3 ; 2 ; 5 . Tính thể tích tứ diện ABCD.
A. 1 6
B. 1
C. 1 3
D. 1 2
Trong không gian với hệ tọa độ Oxyz, cho tứ diện ABCD có
A
0
;
0
;
3
,
B
0
;
3
;
0
,
C
3
;
0
;
0
,
D...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho tứ diện ABCD có A 0 ; 0 ; 3 , B 0 ; 3 ; 0 , C 3 ; 0 ; 0 , D 3 ; 3 ; 3 . Hỏi có bao nhiêu điểm M x ; y ; z (với x, y, z nguyên) nằm trong tứ diện.
A. 4
B. 1
C. 10
D. 7
Đáp án A.
Cách 1:
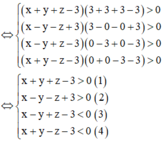
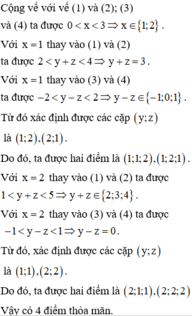
Do các mặt của tứ diện có diện tích bằng nhau nên
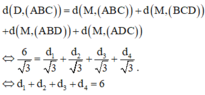
Kiểm tra các trường hợp chỉ có bốn điểm thỏa mãn.
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho tứ diện đều ABCD có A(0;1;2). Gọi H là hình chiếu vuông góc của A lên mặt phẳng (BCD). Cho H(4;-3;-2). Tọa độ tâm I và bán kính R của mặt cầu (S) ngoại tiếp tứ diện ABCD là: A. I(2; -1; 0); R 2
3
B. I(4; -3; -2); R 4
3
C. I(3; -2; -1); R 3
3
D. I(3; -2; -1); R 9
Đọc tiếp
Trong không gian Oxyz, cho tứ diện đều ABCD có A(0;1;2). Gọi H là hình chiếu vuông góc của A lên mặt phẳng (BCD). Cho H(4;-3;-2). Tọa độ tâm I và bán kính R của mặt cầu (S) ngoại tiếp tứ diện ABCD là:
A. I(2; -1; 0); R = 2 3
B. I(4; -3; -2); R = 4 3
C. I(3; -2; -1); R = 3 3
D. I(3; -2; -1); R = 9
Đáp án C
Do ABCD là tứ diện đều nên H là trọng tâm tam giác BCD và I trùng với trọng tâm G của tứ diện ABCD. Ta có:
Từ đó ta có:
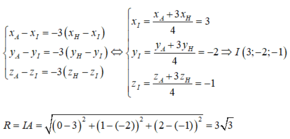
Vậy đáp án C đúng.
Đúng 0
Bình luận (0)