Trong không gian Oxyz cho mặt cầu ( S ) :   ( x - 1 ) 2 + ( y + 2 ) 2 + ( z - 2 ) 2 = 4  và mặt phẳng (P): x-y+2z-1=0 Gọi M là một điểm bất kì trên mặt cầu (S) Khoảng cách từ M đến (P) có giá trị nhỏ nhất bằng

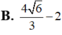
Trong không gian Oxyz, cho mặt cầu ( S ) :   ( x - 1 ) 2 + ( y + 2 ) 2 + ( z - 2 ) 2 = 4  và mặt phẳng (P): x-y+2z-1=0. Gọi M là một điểm bất kì trên mặt cầu (S). Khoảng cách từ M đến (P) có giá trị nhỏ nhất bằng

A.  4 6 3 - 2

B. 0

C.  6 - 2

D.  2 6 - 2

Trong không gian Oxyz, cho mặt cầu (S) có phương trình là: ( x   +   1 ) 2   +   ( y   -   4 ) 2   +   ( z   +   3 ) 2 = 36. Số mặt phẳng (P) chứa trục Ox và tiếp xúc với mặt cầu (S) là:

A. 0

B. 1

C. 2

D. Vô số

Cho mệnh đề:

1) Mặt cầu có tâm I(3;-2;4) và đi qua A(7;2;1) là  ( x - 3 ) 2 + ( y + 2 ) 2 + ( z - 4 ) 2 = 41

2) Mặt cầu có tâm I(2;-1;3) và tiếp xúc với mp (Oxy) là  ( x - 2 ) 2 + ( y - 1 ) 2 + ( z + 3 ) 2 = 9

3) Mặt cầu có tâm I(2;-1;3) và tiếp xúc với mp (Oxz) là  ( x - 2 ) 2 + ( y + 1 ) 2 + ( z - 3 ) 2 = 1

4) Mặt cầu có tâm I(2;-1;3) và tiếp xúc với mp (Oyz) là ( x - 2 ) 2 + ( y + 1 ) 2 + ( z - 3 ) 2 = 4

Số mệnh đề đúng là bao nhiêu:

A. 4

B. 1

C. 2

D. 3

Trong không gian hệ tọa độ Oxyz, cho mặt cầu (S):  ( x - 1 ) 2 + ( y + 2 ) 2 + ( z - 3 ) 2 = 4 . Tìm tọa độ tâm I và bán kính R của mặt cầu đó

A. I(-1;2;3), R=2

B. I(-1;2;-3), R=4

C. I(1;-2;3); R=2

D. I(1;-2;3), R=4

Trong không gian Oxyz, cho mặt cầu (S): (x - 2) 2  + (y + 1) 2  + (z + 2) 2 = 4 và mặt phẳng (P): 4x - 3y + m = 0. Với những giá trị nào của m thì mặt phẳng (P) và mặt cầu (S) có đúng một điểm chung?

A. m=-1

B. m=9 hoặc m=-31

C. m=1 hoặc m=21

D. m=-1 hoặc m=-21

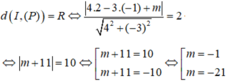
Trong không gian Oxyz, cho mặt cầu (S): ( x - 2 ) 2 + ( y + 1 ) 2 + ( z + 2 ) 2 = 4  và mặt phẳng (P): 4x-3y-m=0. Tìm tất cả các giá trị thực của tham số m để mặt phẳng (P) và mặt cầu (S) có đúng 1 điểm chung

A. m=1

B. m=-1 hoặc m=-21

C. m=1 hoặc m=21

D. m=-9 hoặc m=31

Trong không gian Oxyz, cho mặt cầu S : ( x − 4 ) 2 + ( y + 5 ) 2 + ( z − 3 ) 2 = 4 . Tìm tọa độ tâm I và bán kính R của mặt cầu.

A.  I − 4 ; 5 ; − 3   v à   R = 2

B.  I 4 ; − 5 ; 3   v à   R = 2

C.  I − 4 ; 5 ; − 3   v à   R = 4

D.   I 4 ; − 5 ; 3   v à   R = 4

Trong không gian Oxyz, cho mặt cầu ( S ) : ( x + 2 ) 2 + ( y + 1 ) 2 + ( z - 1 ) 2 = 12 .  Mặt phẳng nào sau đây cắt mặt cầu (S) theo giao tuyến là một đường tròn?

A.  ( P 1 ) : x + y - z + 2 = 0

B.  ( P 2 ) : x + y - z - 2 = 0

C.  ( P 3 ) : x + y - z + 10 = 0

D.  ( P 4 ) : x + y - z - 10 = 0