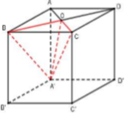
Cho hình lập phương ABCD.A’B’C’D; cạnh bằng a. Gọi O là giao điểm của AC và BD. Thể tích của tứ diện OA’BC bằng
A. a 3 12
B. a 3 24
C. a 3 6
D. a 3 4
Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Tính diện tích S của mặt cầu ngoại tiếp hình lập phương ABCD.A’B’C’D’
A. S = πa 2
B. S = 3 πa 2
C. S = πa 2 3 2
D. S = 4 πa 2 3
Đáp án B
Gọi O, O' lần lượt là tâm các hình vuông ABCD và A'B'C'D'. I là trung điểm đoạn OO'. Khi đó bán kính r của mặt cầu ngoại tiếp hình lập phương ABCD.A'B'C'D' là:

Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Tính diện tích S của mặt cầu ngoại tiếp hình lập phương ABCD.A’B’C’D’
A. S = π a 2
B. S = 3 π a 2
C. S= π a 2 3 2
D. S = 4 π a 2 3
Cho hình lập phương ABCD.A’B’C’D’. Có bao nhiêu hình tứ diện được tạo thành có các đỉnh là các đỉnh của hình lập phương ABCD.A’B’C’D ?
A. 16
B. 96
C. 48
D. 128
Mỗi một hình tứ diện được tạo thành từ 3 đỉnh thuộc một mặt của hình lập phương và một đỉnh từ 4 đỉnh của mặt đối diện ta có C 4 3 . C 4 1 . Ta có 6 trường hợp như thế (6 mặt của hình lập phương). Vậy ta có 16.6 = 96. Chọn A
Cho hình lập phương ABCD.A’B’C’D’ có A’C = 3 . Tính thể tích của hình lập phương.
A. 3 a 3 3
B. a 3
C. 27 a 3
D. 9 a 3
Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Tính diện tích mặt cầu đi qua tất cả các đỉnh của hình lập phương.
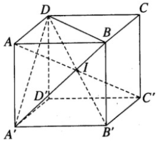
Gọi I là tâm của hình lập phương. Tất cả các đỉnh của hình lập phương đều có khoảng cách đến I bằng 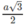 nên chúng nằm trên mặt cầu tâm I bán kính
nên chúng nằm trên mặt cầu tâm I bán kính 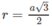
Ta có diện tích mặt cầu đó là S = 4 πr 2 = 3 πa 2
Cho hình lập phương ABCD.A’B’C’D có ẠC' = a (a > 0). Thế tích của khối lập phương đó là
A . a 3 3
B . a 3 3 9
C . a 3
D . 3 a 3 3
Đáp án B
Đặt cạnh của hình lập phương là x
Từ đề bài ta có phương trình:
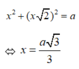
Vậy 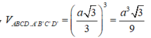
Cho hình lập phương ABCD.A’B’C’D có AC' = a (a>0) Thế tích của khối lập phương đó là
A. a 3 3
B. a 3 3 9
C. a 3
D. 3 a 3 3
Cho hình lập phương ABCD.A’B’C’D’ có thể tích bằng 8a3 .Khi đó độ dài cạnh hình lập phương đã cho bằng
TL :
Gọi cạnh hình lập phương là \(m\)
\(m^3=8a^3=m^3=2^3=2^3.a^3=\left(2a^3\right)=m=2a\)
Vậy độ dài cạnh hình lập phương là \(2a\)
HT
nhanh giúp mik vs
Cho hình lập phương ABCD.A’B’C’D’. Hệ thức nào sau đây đúng?
A. A C ' → = A B → + A C → + A A ' →
B. A C ' → = A B → + C B → + A A ' →
C. A C ' → = A B → + A D → + A A ' →
D. A C ' → = B D → + A C → + A A ' →
Đáp án C.
- Phương pháp: Sử dụng công thức ba điểm và các vectơ bằng nhau.
- Cách giải:
+ Ta có: 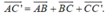
+ Mà:
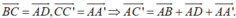
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Hãy xác định tâm và bán kính mặt cầu:
Đi qua 8 đỉnh của hình lập phương.
Tâm là giao điểm các đường chéo (O)
Bán kính mặt cầu là OA = 1/2 AC’
Đường chéo hình vuông cạnh a là a√2 (AC = a√2)
Xét tam giác vuông ACC’ tại C:
⇒ bán kính mặt cầu đi qua 8 đỉnh hình lập phương là (a√3)/2