Cho tứ diện ABCD. Gọi B’ và C’ lần lượt là trung điểm của AB và AC. Khi đó tỉ số thể tích của khối tứ điện AB’C’D và khối tứ diện ABCD bằng:

A. 1 2

B. 1 4

C. 1 6

D. 1 8

Cho tứ diện ABCD. Gọi B’ và C’ lần lượt là trung điểm của AB và AC. Khi đó tỉ số thể tích của khối tứ điện AB’C’D và khối tứ diện ABCD bằng:

A.  1 2

B.  1 4

C.  1 6

D.  1 8

Cho tứ diện ABCD. Gọi B’ và C’ lần lượt là trung điểm của AB và AC. Khi đó tỉ số thể tích của khối tứ điện AB’C’D và khối tứ diện ABCD bằng:

A. 1 2

B.  1 4

C.  1 6

D.  1 8

Cho tứ diện ABCD . Gọi B’ và C’ lần lượt là trung điểm của AB và AC. Khi đó tỉ số thể tích của khối tứ diện AB'C'D' và khối tứ diện ABCD bằng:

A .   1 8

B .   1 6

C .   1 4

D .   1 2

Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, BC và E là điểm đối xứng với B qua D. Mặt phẳng   (MNE) chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh A có thể tích V . Tính V .

A.  7 2 a 3 216

B. 11 2 a 3 216

C. 13 2 a 3 216

D. 2 a 3 18

Cho tứ diện ABCD. Gọi B' và C' lần lượt là trung điểm của AB và AC. Khi đó tỉ số thể tích của khối tứ điện A'B'C'D' và ABCD bằng

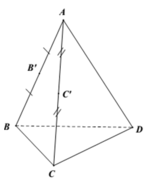
A. x = 1 8  

B.  x = 1 2

C.  x = 1 6

D.  x = 1 4