Mặt cầu bán kính a có diện tích bằng
A. 4 3 πa 2
B. πa 2
C. 4 πa 2
D. πa 3
Những câu hỏi liên quan
Cho hình chóp S.ABC đáy ABC là tam giác vuông tại C, có cạnh AB a = , cạnh bên SA vuông góc mặt phẳng đáy và SA a = 3 . Tính thể tích V khối cầu ngoại tiếp hình chóp.
A. V= 2 2 3 3 a .
B. V= 3 4a .
C. V= 32 3 3 πa .
D. V= 4 3 3 πa .
Cho biết
I
∫
0
π
4
sin
x
+
3
cos
x
sin
x
+
cos
x
d
x
π...
Đọc tiếp
Cho biết I = ∫ 0 π 4 sin x + 3 cos x sin x + cos x d x = πa + lnb (0<a<1; 1<b<3). Tích a.b bằng bao nhiêu?
Trong không gian Oxyz, cho ba điểm A(10;1;1), B(10;4;1) và C(10;1;5). Gọi
S
1
là mặt cầu có tâm A, bán kính bằng 1; gọi
S
2
là mặt cầu có tâm B, bán kính bằng 2 và
S
3
là mặt cầu có tâm C, bán kính bằng 4. Hỏi có bao nhiêu mặt phẳng tiếp xúc với cả ba mặt cầu. A.4. B.7. C.2. D. 3.
Đọc tiếp
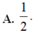
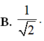
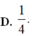
Trong không gian Oxyz, cho ba điểm A(10;1;1), B(10;4;1) và C(10;1;5). Gọi S 1 là mặt cầu có tâm A, bán kính bằng 1; gọi S 2 là mặt cầu có tâm B, bán kính bằng 2 và S 3 là mặt cầu có tâm C, bán kính bằng 4. Hỏi có bao nhiêu mặt phẳng tiếp xúc với cả ba mặt cầu.
A.4.
B.7.
C.2.
D. 3.
Trong không gian với hệ tọa độ Oxyz cho A (1; 2; -3), B (3/2; 3/2; -1/2), C (1; 1; 4), D (5; 3; 0). Gọi (S1) là mặt cầu tâm A bán kính bằng 3, (S2) là mặt cầu tâm B bán kính bằng 3/2. Có bao nhiêu mặt phẳng tiếp xúc với 2 mặt cầu (S1), (S2) đồng thời song song với đường thẳng đi qua 2 điểm C, D. A. 1 B. 2 C. 4 D. Vô số.
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho A (1; 2; -3), B (3/2; 3/2; -1/2), C (1; 1; 4), D (5; 3; 0). Gọi (S1) là mặt cầu tâm A bán kính bằng 3, (S2) là mặt cầu tâm B bán kính bằng 3/2. Có bao nhiêu mặt phẳng tiếp xúc với 2 mặt cầu (S1), (S2) đồng thời song song với đường thẳng đi qua 2 điểm C, D.
A. 1
B. 2
C. 4
D. Vô số.
Chọn A
Cách 1:
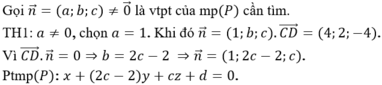
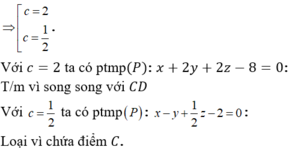
Cách 2: Ta có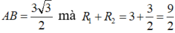 
nên hai mặt cầu cắt nhau theo một đường tròn giao tuyến.
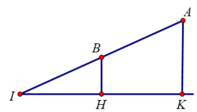
Gọi I = AB ∩ (α) với (α) là mặt phẳng thỏa mãn bài toán.
Hạ vuông góc với mặt phẳng .
Khi đó ta có I nằm ngoài AB và B là trung điểm AI vì
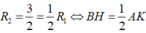
Suy ra I (2;1;2). Gọi (α): a(x-2) + b(y-1) + c(z-2) = 0.
Vì (α) // CD mà 
nên ta có 2a + b - 2c = 0 => b = 2c - 2a
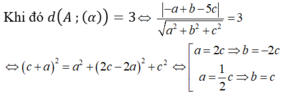
Ta có hai trường hợp:
Nếu b = -2c; a = 2c => (α): 2c (x-2) + 2c (y-1) + c(z-2) = 0 => 2x - 2y + z - 4 = 0
Mặt khác CD // (α) nên CD ∉ (α) loại trường hợp trên.
Nếu b = c; a = c/2 => (α): c/2 . (x-2) + c (y-1) + c(z-2) = 0 => x + 2y + 2z - 8 = 0
Kiểm tra thấy CD ∉ (α) nên nhận trường hợp này. Vậy (α): x + 2y + 2z - 8 = 0
Đúng 0
Bình luận (0)
Có
∫
0
π
4
cos
x
sin
x
+
cos
x
d
x
π
a
+
ln
c
b
với
a...
Đọc tiếp
Có ∫ 0 π 4 cos x sin x + cos x d x = π a + ln c b với a , b , c ∈ ℤ thì a 2 + b + c là:
A. 14
B. 66
C. 66 + 2
D. 70
Có
∫
0
π
4
cos
x
sin
x
+
cos
x
d
x
π
a
+
1
b
ln
c
với
a
,
b
,
c
∈
ℤ
thì...
Đọc tiếp
Có ∫ 0 π 4 cos x sin x + cos x d x = π a + 1 b ln c với a , b , c ∈ ℤ thì a 2 + b + c là:
A. 14
B. 66
C. 66 + 2
D. 70
Có
∫
0
π
4
cos
x
sin
x
+
cos
x
d
x
π
a
+
1
b
ln
c
với
a
,
b
,
c
∈
ℤ
thì
a
2
+
b
+
c
là: A. 14 B. 66 C...
Đọc tiếp
Có ∫ 0 π 4 cos x sin x + cos x d x = π a + 1 b ln c với a , b , c ∈ ℤ thì a 2 + b + c là:
A. 14
B. 66
C. 66 + 2
D. 70
Một mặt cầu có bán kính bằng 2 có diện tích mặt cầu bằng
Đọc tiếp
Một mặt cầu có bán kính bằng 2 có diện tích mặt cầu bằng
1) tính diện tích hình tròn có:a) Bán kính r 0,4 dmb) Bán kính r 3 và 1/4 cmc) Đường kính 7,2 dmd) đường kính 4/5 m2) tính diện tích hình tròn biết chu vi C:a)C 6,28 cmb)C 28,26m3) Tính diện tích của một mặt bàn hình tròn có bán kính 45cm4) Miệng giếng nước là một hình tròn có bán kính 0,7 m. Bao quanh miệng giếng có xây thành giếng roongj,3 m. Tính diện tích của thành giếng đó?
Đọc tiếp
1) tính diện tích hình tròn có:
a) Bán kính r = 0,4 dm
b) Bán kính r = 3 và 1/4 cm
c) Đường kính = 7,2 dm
d) đường kính = 4/5 m
2) tính diện tích hình tròn biết chu vi C:
a)C= 6,28 cm
b)C= 28,26m
3) Tính diện tích của một mặt bàn hình tròn có bán kính 45cm
4) Miệng giếng nước là một hình tròn có bán kính 0,7 m. Bao quanh miệng giếng có xây thành giếng roongj,3 m. Tính diện tích của thành giếng đó?
theo công thức thì bạn lấy
r x r x 3,14 là ra
1. a) 0,5024dm2 b) 36,2984cm2 c) 22,608dm2 d) 14,13m2
2.a) Diện tích hình tròn là: (6,28:2:3,14).1.3,14=3,14cm2
b) Diện tích hình tròn là: (28,26:2:3,14).4,5.3,14=63,585m2
3. Diện tích của mặt bàn hình tròn là: 45.45.3,14=6358,5cm2
4.Diện tích của hinh tròn bé(miệng giếng) đó là: 0,7.0,7.3,14=1,5386cm2
Diện tích của thành giếng đó là:(0,7+0,3).1.3,14)-1,5386=1,6014m2
Đúng 0
Bình luận (0)
Thiết diện qua trục của một hình nón là tam giác đều cạnh bằng 4. Một mặt cầu có diện tích bằng diện tích toàn phần của hình nón. Tính bán kính của mặt cầu. A.
3
B. 4 C.
4
3
D.
2
3
Đọc tiếp
Thiết diện qua trục của một hình nón là tam giác đều cạnh bằng 4. Một mặt cầu có diện tích bằng diện tích toàn phần của hình nón. Tính bán kính của mặt cầu.
A. 3
B. 4
C. 4 3
D. 2 3
Đáp án A
Hình nón có thiết diện qua trục là Δ đều cạnh 4
=> Bán kính đáy r=2 độ dài đường sinh l=4.
Suy ra diện tích toàn phần của hình nón là: S t p = π r l + π r 2 = π .2.4 + π .2 2 = 12 π .
Vậy bán kính mặt cầu là: S = 4 π R 2 ⇒ R = S 4 π = 12 π 4 π = 3
Đúng 0
Bình luận (0)