Các khoảng đồng biến của hàm số y = x 3 + 3 x là
A. ℝ
B. (0;2)
C. ( 0 ; + ∞ )
D. ( - ∞ ; 1 ) và ( 2 ; + ∞ )
Cho hàm số y=f(x) xác định trên ℝ và có đồ thị của hàm số f’(x) và các khẳng định sau:
(1). Hàm số y=f(x) đồng biến trên khoảng 1 ; + ∞
(2). Hàm số y=f(x) nghịch biến trên khoảng - ∞ ; - 2
(3). Hàm số y=f(x) nghịch biến trên khoảng - 2 ; 1 .
(4). Hàm số y = f x 2 đồng biến trên khoảng - 1 ; 0
(5). Hàm số y = f x 2 nghịch biến trên khoảng (1;2)

Số khẳng định đúng là
A. 4
B. 3
C. 2
D. 5
Cho hàm số y = f(x) xác định trên ℝ và có đồ thị của hàm số f ' ( x ) , biết f ( 3 ) + f ( 2 ) = f ( 0 ) + f ( 1 ) và các khẳng định sau:
Hàm số y = f(x) có 2 điểm cực trị.
Hàm số y = f(x) đồng biến trên khoảng ( - ∞ ; 0 ) .
Max [ 0 ; 3 ] f ( x ) = f ( 3 ) .
Min ℝ f ( x ) = f ( 2 ) .
Max [ - ∞ ; 2 ] f ( x ) = f ( 0 ) .

Số khẳng định đúng là
A. 2.
B. 3.
C. 4.
C. 4.
Chọn C.
Dựa vào đồ thị hàm số f ' ( x ) suy ra BBT của hàm số y = f(x)

Khẳng định 1, 2, 5 đúng, khẳng định 4 sai.
Xét khẳng định 3: Ta có:
f ( 3 ) + f ( 2 ) = f ( 0 ) + f ( 1 ) ⇒ f ( 3 ) - f ( 0 ) = f ( 1 ) - f ( 2 ) > 0
Do đó f ( 3 ) > f ( 0 ) ⇒ Vậy khẳng định 3 đúng.
Cho hàm số y=f(x) xác định trên ℝ và có đồ thị của hàm số f'(x), biết f(3)+f(20=f(0)+f(1) và các khẳng định sau:
1) Hàm số y=f(x) có 2 điểm cực trị
2) Hàm số y=f(x) đồng biến trên khoảng - ∞ ; 0
3) M a x 0 ; 3 f x = f 3
4) M a x ℝ f x = f 2
5) M a x - ∞ ; 2 f x = f 0 .
Số khẳng định đúng là

A. 2
B. 3
C. 4
D. 5
Cho hàm số y = x - 2 x - 1 . Xét các mệnh đề sau:
1. Hàm số đã cho đồng biến trên - ∞ ; 1 ∪ 1 ; + ∞ .
2. Hàm số đã cho đồng biến trên ℝ \ { 1 } .
3. Hàm số đã cho đồng biến trên từng khoảng xác định.
4. Hàm số đã cho đồng biến trên các khoảng - ∞ ; - 1 và - 1 ; + ∞ .
Số mệnh đề đúng là:
A. 3
B. 2
C. 1
D. 4
Cho hàm số y = x − 2 x − 1 . Xét các mệnh đề sau:
1. Hàm số đã cho đồng biến trên − ∞ ; 1 ∪ 1 ; + ∞ .
2. Hàm số đã cho đồng biến trên ℝ \ 1 .
3. Hàm số đã cho đồng biến trên từng khoảng xác định.
4. Hàm số đã cho đồng biến trên các khoảng − ∞ ; − 1 và − 1 ; + ∞ .
Số mệnh đề đúng là
A. 3
B. 2
C. 1
D. 4
Cho hàm số y = x − 2 x − 1 . Xét các mênh đề sau
1.Hàm số đã cho đồng biến trên − ∞ ; 1 ∪ 1 ; + ∞ .
2.Hàm số đã cho đồng biến trên ℝ \ 1 .
3.Hàm số đã cho đồng biến trên từng khoảng xác định.
4.Hàm số đã cho đồng biến trên các khoảng − ∞ ; − 1 v à − 1 ; + ∞ .
Số mệnh đề đúng là
A.3
B.2
C.1
D.4
Đáp án C
Có y ' = 1 x − 1 2 . Hàm số đồng biến trên tứng khoảng ( ta chỉ xét khoảng liên tục, không bị ngắt khoảng).
Cho hàm số y = f(x) có đạo hàm f ' x = x 2 x - 9 x - 4 2 . Xét hàm số y = g x = f x 2 trên R. Số phát biểu đúng trong các phát biểu sau là
I. Hàm số y = g x đồng biến trên khoảng 3 ; + ∞
II. Hàm số y = g x nghịch biến trên khoảng - ∞ ; - 3
III. Hàm số y = g x có 5 điểm cực trị
IV. m i n x ∈ ℝ g x = f 9
A. 1
B. 2
C. 3
D. 4
Cho hàm số y = f ( x ) có đạo hàm trên khoảng a ; b . Xét các mệnh đề sau:
I. Nếu hàm số y = f ( x ) đồng biến trên khoảng a ; b thì f ' x > 0 , ∀ x ∈ a ; b .
II. Nếu f ' x < 0 , ∀ x ∈ a ; b thì hàm số y = f ( x ) nghịch biến trên khoảng a ; b .
III. Nếu hàm số y = f ( x ) liên tục trên a ; b và f ' x > 0 , ∀ x ∈ a ; b thì hàm số y = f ( x ) đồng biến trên đoạn a ; b .
Số mệnh đề đúng là:
A. 3
B. 0
C. 2
D. 1
Đáp án là C
I.Sai ví dụ hàm số y = x 3 đồng biến trên
(−¥; +¥) nhưng y' ³ 0, "x Î (−¥; +¥)
II.Đúng
III.Đúng
Cho hàm số f(x) liên tục trên ℝ có f(0)=0 và đồ thị hàm số y = f ' ( x ) như hình vẽ bên
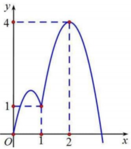
Hàm số y = 3 f ( x ) - x 3 đồng biến trên khoảng
A. 2 ; + ∞
B. - ∞ ; 2
C. (2;0)
D. (1;3)
Đặt g ( x ) = 3 f ( x ) - x 3 . Hàm số ban đầu có dạng y=|g(x)|
Ta có g ' ( x ) = 3 f ' ( x ) - 3 x 2 .
Cho g'(x)=0 ⇔ [ x = 0 x = 1 x = 2

Dễ thấy g(0)=0. Ta có bảng biến thiên
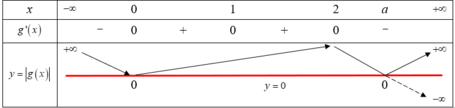
Dựa vào BBT suy ra hàm số y=|g(x)| đồng biến trên khoảng (0;2) và a ; + ∞ với g(a)=0
Chọn đáp án C.
Cho bài toán: “Xét tính đơn điệu của hàm số y = x 2 + 2 x - 3 ” Một bạn học sinh đã làm bài như sau:
Bước 1: Tập xác định: D = ℝ \ ( - 3 ; 1 )
Bước 2: Tìm đạo hàm: y ' = x 2 + 2 x - 3 ' 2 x 2 + 2 x - 3 = x + 1 x 2 + 2 x - 3
Bước 3: y ' = 0 ⇔ x + 1 = 0 x 2 + 2 x - 3 > 0 ⇔ x = 1 x < - 3 ⇔ x ∈ ∅ ; x > 1
Bước 4: Bảng biến thiên:
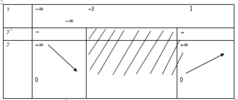
Bước 5: Kết luận:
Vậy hàm số nghịch biến trên nửa khoảng ( - ∞ ; - 3 ] , đồng biến trên nửa khoảng [ 1 ; + ∞ ) . Hỏi bài làm trên đúng hay
sai? Nếu sai thì sai từ bước nào?
A. Bài làm đúng.
B. Sai từ bước 3.
C. Sai từ bước 4.
D. Sai từ bước 5