Mặt cầu (S) có diện tích bằng 20 π , thể tích khối cầu (S) bằng
A. 20 π 5 3
B. 20 π 5
C. 20 π 3
D. 4 π 5 3
Cho khối cầu có diện tích S=8 π , thể tích V của khối cầu bằng:
![]()
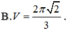
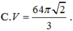
![]()
Cho mặt cầu (S) có bán kính R = 5 (cm). Mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là đường tròn (C) có chu vi bằng 8 π (cm). Bốn điểm A, B, C, D thay đổi sao cho A, B, C thuộc đường tròn (C), điểm D thuộc (S) (D không thuộc đường tròn (C)) và tam giác ABC là tam giác đều. Thể tích lớn nhất của khối tự diện ABCD bằng bao nhiêu?
A. 32 3 ( c m 3 )
B. 60 3 ( c m 3 )
C. 20 3 ( c m 3 )
D. 96 3 ( c m 3 )
Cho hình cầu có diện tích mặt cầu là 64 π ( c m 2 ). Tính thể tích khối cầu?
A. 256 π 3 c m 3
B. 256 π c m 3
C. 64 π 3 c m 3
D. Đáp án khác
Cho mặt cầu (S) có diện tích bằng 4 π . Thể tích khối cầu (S) bằng
![]()
![]()
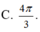
![]()
Một hình hộp chữ nhật có ba kích thước lần lượt là a, b, c. Gọi (S) là mặt cầu đi qua 8 đỉnh của hình hộp chữ nhật đó. Diện tích của mặt cầu (S) theo a, b, c là:
A. π ( a 2 + b 2 + c 2 ) B. 2 π ( a 2 + b 2 + c 2 )
C. 4 π ( a 2 + b 2 + c 2 ) D. π /2.( a 2 + b 2 + c 2 )
Chọn A.
Đường kính của mặt cầu (S) chính là đường chéo của hình hộp chữ nhật, nên mặt cầu (S) có bán kính
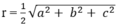
Do đó diện tích mặt cầu (S) là: S = 4 πr 2 = π( a 2 + b 2 + c 2 )
Cắt mặt cầu (S) bằng một mặt phẳng cách tâm một khoảng bằng 4cm được thiết diện là một hình tròn có diện tích 9 π cm 2 . Tính thể tích khối cầu (S).
![]()
![]()
![]()
![]()
Cho một khối cầu có thể tích bằng 500 π 3 . Tính diện tích S của mặt cầu đó.
![]()
![]()
![]()
![]()
Cho một khối cầu có thể tích bằng 500 π 3 . Tính diện tích S của mặt cầu đó
A. S = 75 π .
B. S = 100 π .
C. S = 50 π .
D. S = 25 π .
Đáp án B
V = 4 3 π R 3 = 500 π 3 ⇒ R = 5 S = 4 π R 2 = 100 π
Cho một khối cầu có thể tích bằng 500 π 3 . Tính diện tích S của mặt cầu đó
A. S = 75 π
B. S = 100 π
C. S = 50 π
D. S = 25 π