Trên mặt phẳng tọa độ các điểm A,B,C lần lượt là điểm biểu diễn các số phức i 3 , 3 − i 1 − i , 5 + 3 i 1 − i 2 .  Khi đó tam giác ABC.

A. vuông cân tại B

B. đều

C. vuông cân tại A

D. vuông cân tại C

Trên mặt phẳng tọa độ các điểm A,B,C lần lượt là điểm biểu diễn các số phức  i 3 , 3 - i 1 - i , 5 + 3 i 1 - i 2   . Khi đó tam giác ABC

A. đều

B. vuông cân tại C

C. vuông cân tại B

D. vuông cân tại A

Trên mặt phẳng tọa độ các điểm A,B,C lần lượt là điểm biểu diễn các số phức i 3 ,   3 - i 1 - i ,   5 + 3 i 1 - i 2 . Khi đó tam giác ABC

A. đều

B. vuông cân tại C

C. vuông cân tại B

D. vuông cân tại A

Trong mặt phẳng tọa độ cho các điểm A, B, C lần lượt là điểm biểu diễn các số phức - 1 + 3 i 1 - i ; 5 i 1 + 2 i ; 3 i . Khi đó tam giác ABC:

A. Vuông tại A.

B. Vuông cân tại C.

C. Tam giác đều

D. Vuông tại C.

Trong mặt phẳng tọa độ cho các điểm A, B, C lần lượt là điểm biểu diễn các số phức - 1 + 3 i 1 - i ,   5 i 1 + 2 i , 3 i . Khi đó tam giác ABC

A. Vuông tại A.

B. Vuông cân tại C

C. Tam giác đều

D. Vuông tại C.

Cho các số phức z1,z2 có điểm biểu diễn trên mặt phẳng tọa độ lần lượt là M,N. Gọi P là trung điểm của MN, khi đó P biểu diễn số phức

A..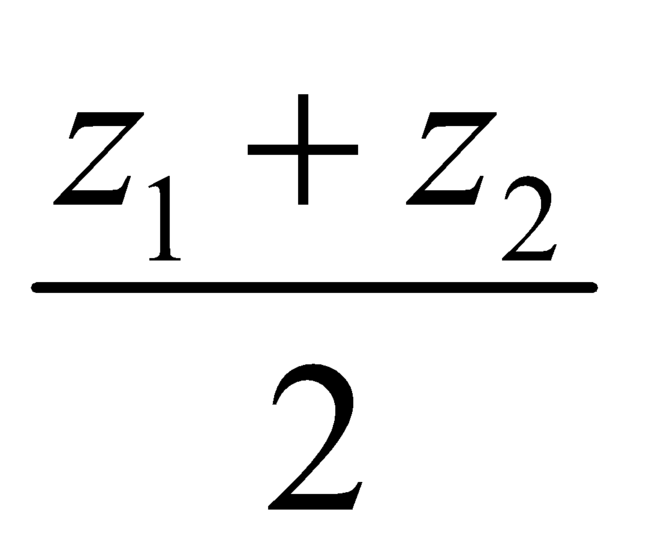

B..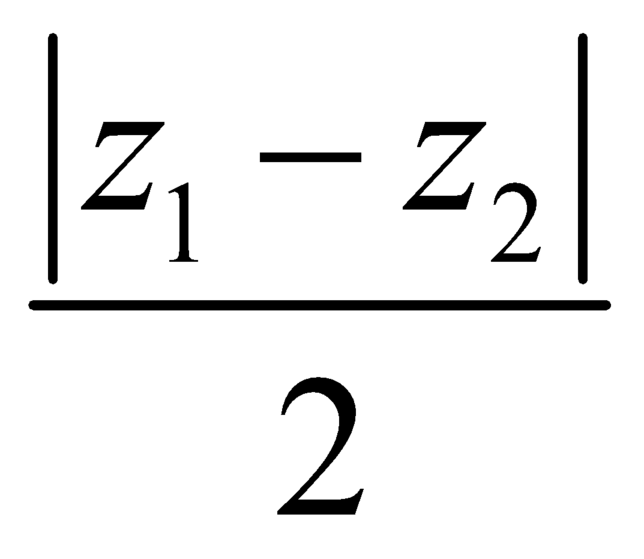

C..

D..

Gọi điểm A,B lần lượt biểu diễn các số phức z và z ' = 1 + i 2 z ; (z khác 0) trên mặt phẳng tọa độ (A,B,C và A',B',C' đều không thẳng hàng). Với O là gốc tọa độ, khẳng định nào sau đây đúng?

A. Tam giác OAB đều

B.  Tam giác OAB vuông cân tại O

C. Tam giác OAB vuông cân tại B

D. Tam giác OAB vuông cân tại A

Cho số phức z = 1 + 3 i . Gọi A,B lần lượt là điểm biểu diễn của các số phức (1+i)z và (3-i)z trong mặt phẳng tọa độ Oxy. Tính độ dài đoạn AB.

Cho số phức z = 1 + 3 i . Gọi A,B lần lượt là điểm biểu diễn của các số phức (1+i)z và (3-i)z trong mặt phẳng tọa độ Oxy. Tính độ dài đoạn AB