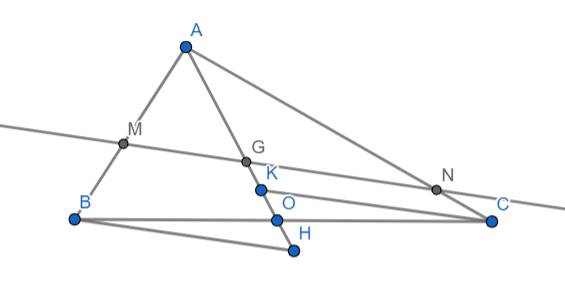
Xét 2 tam giác AMG và ABH ta có:

\(\widehat{BAH}\) chung 

\(\widehat{AMG}=\widehat{ABH}\) (cặp góc đồng vị do BH//MG) 

\(\Rightarrow\Delta AMG\sim\Delta ABH\left(g.g\right)\) 

\(\Rightarrow\dfrac{AB}{AM}=\dfrac{AH}{AG}\) (1) 

Xét 2 tam giác ANG và ACK có:

\(\widehat{CAK}\) chung 

\(\widehat{ANG}=\widehat{ACK}\) (cặp góc đồng vị do CK//GN) 

\(\Rightarrow\Delta ANG\sim\Delta ACK\left(g.g\right)\)

\(\Rightarrow\dfrac{AC}{AN}=\dfrac{AK}{AG}\) (2) 

Xét hai tam giác BOH và COK ta có: 

\(\widehat{BOH}=\widehat{COK}\) (đối đỉnh) 

\(BO=CO\) (AO là đường trung tuyến nên O là trung điểm của BC) 

\(\widehat{HBO}=\widehat{KCO}\) (so le trong vì BH//MN và CK//MN ⇒ BH//CK) 

\(\Rightarrow\Delta BOH=\Delta COK\left(g.c.g\right)\) 

\(\Rightarrow HO=OK\) (hai cạnh t.ứng) 

\(\Rightarrow HK=2HO\)

Ta lấy (1) + (2) \(\Rightarrow\dfrac{AB}{AM}+\dfrac{AC}{AN}=\dfrac{AH+AK}{AG}=\dfrac{AH+AH+HK}{AG}=\dfrac{2AH+HK}{AG}\) 

\(=\dfrac{2AH+2HO}{AG}=\dfrac{2\left(AH+HO\right)}{AG}=\dfrac{2AO}{AG}\) 

Mà G là trọng tâm của tam giác ABC \(\Rightarrow AO=\dfrac{3}{2}AG\) 

\(\Rightarrow\dfrac{AB}{AM}+\dfrac{AC}{AN}=\dfrac{2\cdot\dfrac{3}{2}AG}{AG}=2\cdot\dfrac{3}{2}=3\left(đpcm\right)\)  

Gọi I,J,K lần lượt là trung điểm của các cạnh BC,CA,AB; các đường thẳng d1,d2 đi qua G và song song với AB,AC và cắt AC,AB tại L,H. Khi đó ta có: GL//AB=>AB/GL=BJ/GJ=3; GL//AM=>GL/AM=NG/MN. Nhân hai đẳng thức theo vế thì được AB/AM=3NG/MN (*). Một cách tương tự ta cũng chứng minh được AC/AN=3MG/MN (*). Cộng (*) và (**) theo vế thì được AB/AM+AC/AN=3(NG+MG)/MN=3.

Gọi J là trung điểm BC. Khi đó AJ là trung tuyến. Vậy thì AG = 2GJ.     (1)

Xét tứ giác BIKC có BI cùng CK cùng song song với AG nên BI // CK hay BIKC là hình thang.

Xét hình thang BIKC có :

J là trung điểm BC

GJ // BI // KC 

Suy ra GJ là đường trung bình hình thang BIKC.

Từ đó ta có: \(BI+CK=2GJ\)                    (2)

Từ (1) và (2) suy ra \(BI+KC=AG\)