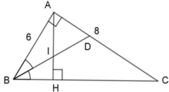
+ Áp dụng định lý Pitago trong tam giác vuông ABC ta có:

A B 2 + A C 2 = B C 2   ⇔ 6 2 + 8 2 = B C 2   ⇔ B C 2 = 100 ⇒ B C = 10 c m

+ Vì BD là đường phân giác của tam giác ABC nên áp dụng tính chất đường phân giác của tam giác, ta có:

B A A D = B C C D ⇔ B A A D = B C C A − A D ⇔ 6 A D = 10 8 − A D

=> AD = 3cm => DC = AC - AD = 8 - 3 = 5cm

Đáp án D.

a/ \(BD\) là đường phân giác \(\widehat{BAC}\)

\(\to\dfrac{DA}{DC}=\dfrac{BA}{BC}\) hay \(\dfrac{DA}{DC}=\dfrac{6}{10}=\dfrac{3}{5}\)

\(\to\dfrac{DA}{3}=\dfrac{DC}{5}=\dfrac{DA+DC}{3+5}=\dfrac{AC}{8}=\dfrac{8}{8}=1\)

\(\to\begin{cases}DA=3\\DC=5\end{cases}\)

b/ \(S_{\Delta ABC}=\dfrac{1}{2}.AB.AC=\dfrac{1}{2}.AH.BC\)

\(\to AB.AC=AH.BC\)

\(\to \dfrac{AB.AC}{BC}=AH=\dfrac{6.8}{10}=3,2(cm)\)

b) Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:

\(AH\cdot BC=AB\cdot AC\)

\(\Leftrightarrow AH\cdot10=6\cdot8=48\)

hay AH=4,8(cm)

Vậy: AH=4,8cm

a) Xét △ABC vuông tại A có:

BC² = AC² + AB² (ĐL Pytago)

BC² = 8² + 6²

BC² = 100

BC = 10 cm

Vậy BC = 10 cm

b) Xét △ABD và △EBD có:

góc BAD = góc BED (=90°)

BD chung

góc ABD = góc EBD (BD là tia p/g của góc ABC)

=> △ABD = △EBD (ch-gn)

c) Câu này đề bài có cho thiếu gia thiết ko bạn chứ vẽ hình chả biết ntn á

Câu 3 là phần c nha

a) Xét △ABC vuông tại A có:

BC² = AC² + AB² (ĐL Pytago)

BC² = 8² + 6²

BC² = 100

BC = 10 cm

Vậy BC = 10 cm

b) Xét △ABD và △EBD có:

góc BAD = góc BED (=90°)

BD chung

góc ABD = góc EBD (BD là tia p/g của góc ABC)

=> △ABD = △EBD (ch-gn)

 cre baji

a: BC=10cm

Xet ΔABC vuông tại A và ΔHBA vuông tại H có

góc B chung

=>ΔABC đồng dạngvới ΔHBA

b: AH=6*8/10=4,8cm

BH=6^2/10=3,6cm

CH=10-3,6=6,4cm

\(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)

BD là phân giác

=>DA/AB=DC/BC

=>DA/3=DC/5=8/8=1

=>DA=3cm; DC=5cm

a: Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:

\(BC^2=AB^2+AC^2\)

\(\Leftrightarrow BC^2=100\)

hay BC=10cm

Xét ΔABC có BD là đường phân giác ứng với cạnh AC

nên \(\dfrac{AD}{AB}=\dfrac{CD}{BC}\)

hay \(\dfrac{AD}{6}=\dfrac{CD}{10}\)

mà AD+CD=8

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{AD}{6}=\dfrac{CD}{10}=\dfrac{AD+CD}{6+10}=\dfrac{8}{16}=\dfrac{1}{2}\)

Do đó: AD=3cm; CD=5cm

b: Xét ΔABC vuông tại A và ΔHBA vuông tại H có 

\(\widehat{ABC}\) chung

Do đó: ΔABC\(\sim\)ΔHBA

Suy ra: \(\dfrac{BA}{BH}=\dfrac{BC}{BA}\)

hay \(AB^2=BH\cdot BC\)

c) Ta có: \(\widehat{ABD}=\widehat{DBC}\)( BD là phân giác )\(\Rightarrow90^0-\widehat{ABD}=90^0-\widehat{DBC}\Rightarrow\widehat{BIH}=\widehat{ADI}\Rightarrow\widehat{AID}=\widehat{ADI}\Rightarrow\Delta ADI\) cân tại A\(\Rightarrow AI=AD\Rightarrow\dfrac{AB}{AI}=\dfrac{AB}{AD}\)

Xét Δ ABI và Δ CBD có:

\(\widehat{BAI}=\widehat{BCD}\left(\Delta ABC\sim\Delta HBA\right)\)

\(\dfrac{AB}{AI}=\dfrac{BC}{CD}\left(=\dfrac{AB}{AD}\right)\)

\(\Rightarrow\Delta ABI\sim\Delta CBD\left(c.g.c\right)\)

d) Xét ΔABH có:

BI là tia phân giác của \(\widehat{ABH}\)

\(\Rightarrow\dfrac{IH}{IA}=\dfrac{BH}{AB}\left(1\right)\)( tính chất tia phân giác)

Xét ΔABC có:

BD là tia phân giác của \(\widehat{ABC}\)

\(\Rightarrow\dfrac{AD}{DC}=\dfrac{AB}{BC}\left(2\right)\)( tính chất tia phân giác)

Ta có: \(\dfrac{BH}{AB}=\dfrac{AB}{BC}\left(\Delta ABC\sim\Delta HBA\right)\left(3\right)\)

Từ \(\left(1\right),\left(2\right),\left(3\right)\Rightarrow\dfrac{IH}{IA}=\dfrac{AD}{DC}\left(đpcm\right)\)

c: Xét ΔABI và ΔCBD có 

\(\widehat{ABI}=\widehat{CBD}\)

\(\widehat{BAI}=\widehat{BCD}\left(=90^0-\widehat{ABH}\right)\)

Do đó: ΔABI\(\sim\)ΔCBD

d: Xét ΔBHA có BI là đường phân giác ứng với cạnh AH

nên \(\dfrac{IH}{IA}=\dfrac{BH}{BA}\left(1\right)\)

Xét ΔBAC có BD là đường phân giác ứng với cạnh AC

nên \(\dfrac{AD}{DC}=\dfrac{AB}{BC}\left(2\right)\)

Ta có: \(AB^2=BH\cdot BC\)

nên \(\dfrac{BH}{BA}=\dfrac{AB}{BC}\left(3\right)\)

Từ \(\left(1\right),\left(2\right),\left(3\right)\) suy ra \(\dfrac{IH}{IA}=\dfrac{AD}{DC}\)