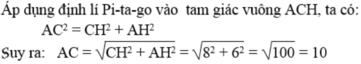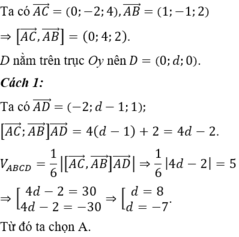Tứ giác ABCD có tọa độ các đỉnh như sau A(0;2); B(3; 0); C(0;-2) ; D(-3;0).Tứ giác ABCD là hình gì ? Tính chu vi của tứ giác đó.

Những câu hỏi liên quan
tứ giác ABCD có tọa độ các đỉnh như sau A(0:2) , B(3:0) , C(0:-2) , D(-3:0) . tứ giác ABCD là hình gì ? Tính chu vi của tứ giác đó.
Tứ giác ABCD có tọa độ các đỉnh như sau : \(A\left(0;2\right),B\left(3;0\right),C\left(0;-2\right),D\left(-3;0\right)\). Tứ giacs ABCD là hình gì ? Tính chu vi tứ giác đó ?
tứ giác ABCD có tọa độ các đỉnh A(0,-4),B(3,0),C(0,4),D(-3,0). Tứ giác ABCD là hình gì ? Tính chu vi của tứ giác đó
Ta có: A(0;-4) và C(0;4) là hai điểm đối xứng qua O(0;0)
⇒ OA = OC
B(3;0) và D(-3; 0) là hai điểm đối xứng qua O(0;0)
⇒ OB = OD
Tứ giác ABCD là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường)
Lại có: Ox ⊥ Oy hay AC ⊥ BD.
Vậy tứ giác ABCD là hình thoi
Trong Δ∆OAB vuông tại O, theo định lý Pi-ta-go ta có:
AB2=OA2+OB2
AB2=42+32 = 16 + 9 = 25
AB = √25
Vậy chu vi của hình thoi bằng 4√25
Đố em tìm thấy vị trí của "kho báu" trên hình 11, biết rằng kho báu nằm tại giao điểm các đường chéo của tứ giác ABCD, trong đó các đỉnh của tứ giác có tọa độ như sau: A(3; 2), B(2; 7), C(6; 8), D(8; 5).
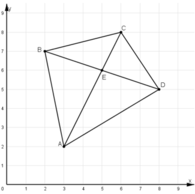
+ Xác định các điểm A, B, C, D trong hệ trục tọa độ như trên hình vẽ.
+ Hai đường chéo của tứ giác là AC và BD.
+ Vị trí kho báu là giao điểm của AC và BD và là điểm E trên hình vẽ.
+ Nhìn trên hình vẽ thấy điểm E có tọa độ (5; 6)
Vậy vị trí tọa độ của kho báu là (5; 6)
Đúng 0
Bình luận (0)
Trong mpOxy, cho HBH ABCD có phương trình đường chéo AC:x-y+1=0, điểm G(1;4) là trọng tâm tam giác ABC,điểm E(0;3) thuộc đường cao kẻ từ D của tam giác ACD.Tìm tọa độ các đỉnh HBH biết diện tích tứ giác AGCD bằng 32 và đỉnh A có tung độ dương.
Trên mặt phẳng tọa độ Oxy cho bốn điểm A, B, C, D có tọa độ nguyên như sau:
A(4;5) B(1;-1) C(4;-4) D(7; -1).
Tính (theo độ, phút) các góc của tứ giác ABCD bằng máy tính bỏ túi.
Hai đường chéo AC và BD vuông góc với nhau tại I.
- Đường thẳng AB có hệ số góc bằng 2, do đó ta có
tgα = 2 ⇒ α = 63 ° 26 ' (tính trên máy tính bỏ túi).
Suy ra ∠ (ABD) ≈ 63 ° 26 '
Tam giác ABD cân, nên cũng có ∠ (ADB) ≈ 63 ° 26 '
Từ đó suy ra ∠ (BAD) = 180 ° - 2. 63 ° 26 ' ≈ 53 ° 8 '
Đúng 0
Bình luận (0)
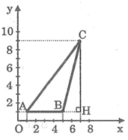
Trong mặt phẳng tọa độ, các đỉnh của tam giác ABC có tọa độ như sau: A(1; 1), B(5; 1), C(7; 9)
Hãy tính: Độ dài của cạnh AC
Trong không gian Oxyz cho tứ diện ABCD có thể tích
V
5
, các đỉnh
A
2
;
1
;
−
1
,
B
3
;
0
;
1
,
C
2
;
−...
Đọc tiếp
Trong không gian Oxyz cho tứ diện ABCD có thể tích V = 5 , các đỉnh A = 2 ; 1 ; − 1 , B = 3 ; 0 ; 1 , C = 2 ; − 1 ; 3 , đỉnh thứ tư D nằm trên trục Oy và có tung độ dương. Tìm tọa độ của D.
A. D = 0 ; 8 ; 0
B. D = 0 ; 7 ; 0
C. D = 0 ; 7 4 ; 0
D. D = 0 ; 17 4 ; 0
1. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có cạnh AC đi qua điểm M (0;-1). Biết AB 2AM, phương trình đường phân giác trong AD : x-y 0, phương trìn đường cao CH: 2x+y+3 0. Tìm tọa độ các đỉnh A,B,C.2. Trong mặt phẳng tọa độ Oxy, cho hình vuông ABCD tâm I (-1;1). Gọi M nằm trên cạnh CD sao cho MC 2 MD. Tìm tọa độ điểm C biết đường thẳng AM có phương trình 2x-y0,điểm A có hoành độ dương
Đọc tiếp
1. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có cạnh AC đi qua điểm M (0;-1). Biết AB =2AM, phương trình đường phân giác trong AD : x-y =0, phương trìn đường cao CH: 2x+y+3 =0. Tìm tọa độ các đỉnh A,B,C.
2. Trong mặt phẳng tọa độ Oxy, cho hình vuông ABCD tâm I (-1;1). Gọi M nằm trên cạnh CD sao cho MC =2 MD. Tìm tọa độ điểm C biết đường thẳng AM có phương trình 2x-y=0,điểm A có hoành độ dương