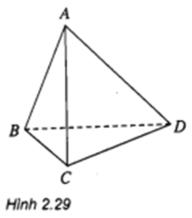
Cho tứ diện ABCD, chứng minh hai đường thẳng AB và CD chéo nhau. Chỉ ra cặp đường thẳng chéo nhau khác của tứ diện này (h.2.29).
Cho hai đoạn thẳng AB và CD chéo nhau, AC là đường vuông góc chung của chúng. Biết rằng AC = h, AB = a, CD = b và góc giữa hai đường thẳng AB và CD bằng 600. Hãy tính thể tích của khối tứ diện ABCD.
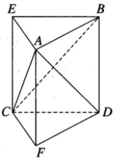
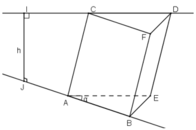
Dựng BE song song và bằng DC, DF song song và bằng BA. Khi đó, ABE.FDC là một lăng trụ đứng.
Ta có:
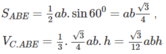
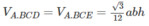
Cho hai đường thẳng AB và CD chéo nhau, AC là đường vuông góc chung của chúng. Biết AC = h, AB = a, CD = b và góc giứa hai đường thẳng AB và CD bằng \(60^0\). Hãy tính thể tích của khối tứ diện ABCD ?
Dựng BE song song và bằng DC, DF song song và bằng BA. Khi đó ABE.FDC là một lăng trụ đứng

Ta có :
\(S_{ABE}=\dfrac{1}{2}ab.\sin60^0=ab\dfrac{\sqrt{3}}{4}\)
\(V_{C.ABE}=\dfrac{1}{3}.\dfrac{\sqrt{3}}{4}ab.h=\dfrac{\sqrt{3}}{12}abh\)
Từ đó suy ra :
\(V_{A.BCD}=V_{A.BCE}=\dfrac{\sqrt{3}}{12}abh\)
Cho hai đường thẳng chéo nhau d và d’. Đoạn thẳng AB có độ dài bằng a trượt trên d, đoạn thẳng CD có độ dài bằng b trượt trên d’. Chứng minh rằng khối tứ diện ABCD có thể tích không đổi.
Gọi h là khoảng cách hai đường thẳng d và d’, gọi α là góc tạo bởi hai đường thẳng d và d’.
Lần lượt vẽ hai hình bình hành BACF và ACDE.
Khi đó, ABE.CFD là hình lăng trụ tam tam giác có chiều cao h; AE = CD = b và 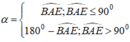
Gọi S là diện tích đáy của hình lăng trụ .
Ta chia hình lăng trụ ABE. CFD thành ba hình chóp tam giác là: D. ABE, B. CFD, D.ABC. Ta có:
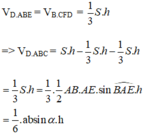
Do đó, thể tích khối tứ diện ABCD không đổi.
Cho hai đường thẳng chéo nhau d và d'. Đoạn thẳng AB có độ dài a trượt trên d, đoạn thẳng CD có độ dài b trượt trên d'. Chứng minh rằng khối tứ diện ABCD có thể tích không đổi ?
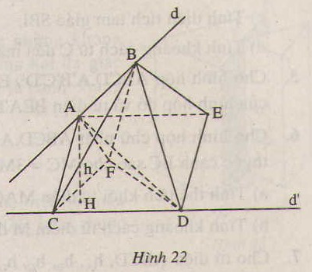
Gọi h là độ dài đường vuông góc chung của d và d’, α là góc giữa hai đường thẳng d và d’. Qua B, A, C dựng hình bình hành BACF. Qua A,C, D dựng hình bình hành ACDE.
Khi đó CFD.ABE là một hình lăng trụ tam giác. Ta có:
VDABC=VDFCB=VBCDF
= VCFD.ABE
= hSFCD=
h.
ab. sinα
=h. ab. sinα (là một số không đổi).
Xem thêm tại: http://loigiaihay.com/cau-6-trang-26-sgk-hinh-hoc-12-c47a2782.html#ixzz4cxsiVwHA
Cho hình thoi ABCD, gọi O là giao điểm của hai đường chéo. Vẽ đường thẳng qua và song với AC, vẽ đường thẳng qua C và song song với BD, hai đường chéo này cắt nhau tại K a) Chứng minh rằng tứ giác OBKC là hình chữ nhật b) Chứng minh tứ giác ABKO là hình bình hành c) Tìm điều kiện về hai đường chéo của hình thoi ABCD để tứ giác OBKC kà hình vuông
THAM KHẢO
a) BK//OC, CK//OB.
Mà OB ^OC Þ OBKC là hình chữ nhật.
b)ABCD là hình thoi nên AB = BC. OBKC là hình chữ nhật nên KO =BC.
Þ KO = BC Þ ĐPCM.
c) nếu OBKC là hình vuông thì OB = OC Þ BD = AC. Vậy ABCD là hình vuông
tứ giác ABCD có AB=CD. Chứng minh rằng đường thẳng đi qua trung điểm của hai đường chéo tạo với AB và CD các góc bằng nhau
Cho tứ giác lồi ABCD. Qua trung điểm của đường chéo BD dựng đường thẳng song song với đường chéo AC , đường thẳng này cắt đoạn thẳng AD tại E. Chứng minh rằng CE chia tứ giác thành 2 phần có diện tích bằng nhau.
toán 8 đó mọi người, giải hộ
Cho tứ giác ABCD nội tiếp đường tròn tâm O. Hai đường chéo AC và BD vuông góc với nhau tại E. Chứng mình rằng một đường thẳng qua E và vuông gốc với một cạnh của tứ giác khi và chỉ khi đường thẳng đó đi qua trung điểm của cạnh đối diện của tứ giác
Cho tứ giác lồi ABCD, AB=CD, Chứng minh đường thẳng đi qua trung điểm của hai đường chéo tạo với CD các góc bằng nhau
Gọi trung điểm dường cheo AC, BD lần lượt là M, N
MN cắt AB, CD lần lượt ở I, K
Ta cần chứng minh góc NIB = góc MKC
Lấy H là trung điểm BC. Nối MH, NH.
Xét tam giac ABC có AM = MC ; CH = HB => MH là đường trung bình tam giác ABC => MH =AB/2 (1) và MH // AB => góc KMH = góc INH (2)
chung minh tuong tu ta có: NH = CD/2 (3)và NH // CD =>góc INH = góc MKC (4)
Mat khac từ (1)và (3) ta có NH = MH vì đều bằng một nửa AB và CD => tam giác MHN cân tại H => góc NMH = góc MNH =>góc KMH = góc INH (vì kể với 2 góc bằng nhau) (5)
Từ (3)(4)(5) => góc MKC = góc NIB (đpcm)