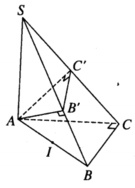
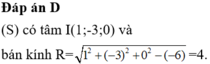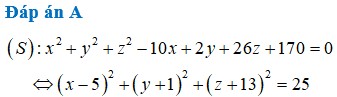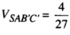Trong không gian Oxyz, cho S(0; 0; 2), A(0; 0; 0), B(1; 2; 0), C(0; 2; 0). Chứng minh các điểm A, B, C, B', C' cùng thuộc một mặt cầu. Viết phương trình của mặt cầu đó và phương trình của mặt phẳng tiếp xúc với mặt cầu đó tại C'.

Những câu hỏi liên quan
Trong không gian Oxyz, cho mặt cầu (S): x²+y²+z²-2x+6y-6=0. Bán kính của (S) bằng:
A. √46
B. 16
C. 2
D. 4.
Trong không gian Oxyz, cho mặt cầu (S):
x
2
+
y
2
+
z
2
-
2
y
+
4
z
0
. Thể tích khối cầu (S) là A.
12
π
B.
36
π
C.
24
π
D.
25
π
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S): x 2 + y 2 + z 2 - 2 y + 4 z = 0 . Thể tích khối cầu (S) là
A. 12 π
B. 36 π
C. 24 π
D. 25 π
Trong không gian Oxyz, cho mặt cầu (S) có phương trình: x 2 + y 2 + z 2 = 4 a 2 (a > 0).
Trong không gian Oxyz, cho mặt cầu
(
S
)
:
x
2
+
y
2
+
z
2
-
2
x
+
4
y
-
4
0
Thể tích của khối cầu (S) bằng A.
36
π
B.
9
π
C.
32
π
D.
16...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu ( S ) : x 2 + y 2 + z 2 - 2 x + 4 y - 4 = 0 Thể tích của khối cầu (S) bằng
A. 36 π
B. 9 π
C. 32 π
D. 16 π
Mặt cầu (S) có tâm I(1;-2;0), R=3
![]()
Chọn đáp án A.
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho mặt cầu
(
S
)
:
x
2
+
y
2
+
z
2
-
10
x
+
2
y
+
26
z
+
170
0
, tọa độ tâm của (S) là A. (5;-1;-13) B. (-5;1;13) C. (10;-2;-26) D. (-10;2;26)
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu ( S ) : x 2 + y 2 + z 2 - 10 x + 2 y + 26 z + 170 = 0 , tọa độ tâm của (S) là
A. (5;-1;-13)
B. (-5;1;13)
C. (10;-2;-26)
D. (-10;2;26)
Trong không gian Oxyz, cho S(0; 0; 2), A(0; 0; 0), B(1; 2; 0), C(0; 2; 0). Tính thể tích tứ diện SAB'C'
Trong không gian Oxyz, cho mặt cầu (S):
x
2
+
y
2
+
z
2
-
2
x
-
4
y
-
6
z
-
11...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S): x 2 + y 2 + z 2 - 2 x - 4 y - 6 z - 11 = 0 . Tọa độ tâm T của (S) là
A. T(2;4;6).
B. T(1;2;3).
C. T(-2;-4;-6).
D. T(-1;-2;-3).
Trong không gian Oxyz, cho mặt cầu (S): x 2 + y 2 + z 2 - 2 x - 3 = 0 . Bán kính mặ cầu bằng
A. 3
B. 4
C. 2
D. 5
Trong không gian Oxyz, cho mặt cầu (S) có phương trình
x
2
+
y
2
+
z
2
-
2
z
-
4
y
-
6
z
0
.Tính diện tích mặt cầu(S). A.
42
π
B.
36
π
C.
9
π
D.
12
π
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S) có phương trình x 2 + y 2 + z 2 - 2 z - 4 y - 6 z = 0 .Tính diện tích mặt cầu(S).
A. 42 π
B. 36 π
C. 9 π
D. 12 π
Đáp án B
Ta có:
S : x - 1 2 + y - 2 2 ÷ z - 3 2 = 9 ⇒ S có bán kính R = 3
Diện tích mặt cầu (S) là: 4 π · 3 2 = 36 π .
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho mặt cầu (S) có phương trình
x
2
+
y
2
+
z
2
-
2
x
-
4
y
-
6
z
...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S) có phương trình x 2 + y 2 + z 2 - 2 x - 4 y - 6 z = 0 . Tính diện tích mặt cầu (S).
A. 42 π
B. 36 π
C. 9 π
D. 12 π
Đáp án B
Ta có:
![]()
=> (S) có bán kính R =3
Diện tích mặt cầu là: 4 π . 3 2 = 36 π
Đúng 0
Bình luận (0)