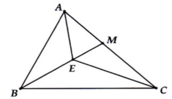
Cho hình vẽ bên. Hãy so sánh:
a) A E M ^ và A B M ^
b) A E C ^ và A B C ^
cho hình vẽ bên. trong đó ABCD là hình chữ nhật. AB kéo dài để có AB= BE. đoạn thẳng ED căt BC tại M. hãy
a, so sánh BEM và CDM
b, so sánh MB VÀ MC
c, So sánh bh và ck
Hình thì bạn tự vẽ nhé. Mk k bt vẽ ở trên này :))
a) - Có AB=BE (gt) mà 2 chiều rộng hình chữ nhật thì = nhau -> AB= BE= CD ->BE=CD
- Vì là HCN -> góc ABC=góc DCB= 90 độ
mà góc ABC và góc MBE là 2 góc kề bù => góc ABC= góc MBE= 180/2= 90 độ => góc MBE= DCB= 90 độ
- Xét tam giác BME và tam giác CMD có:
Góc MBE+ BME+ E= 180 độ (tổng 3 góc của 1 tam giác) và góc C+ CMD+D= 180 độ (tổng 3 góc của 1 tam giác)
mà góc MBE=DCB (cmt), BME=CMD (2 góc đối đỉnh) => góc E= MDC
- Xét tam giác BEM và tam giác CDM có:
góc E= góc MDC (cmt)
BE= CD (cmt)
góc MBE= góc DCB (=90 độ, cmt)
=> Tam giác BEM= tam giác CDM (g-c-g)
b) Vì tam giác BEM= tam giác CDM ( cm câu a) => MB= MC (2 cạnh tương ứng)
c) Câu này thì mk k làm đc tại hình như bạn ghi đề bài bị thiếu hay sai ý. Mk đọc k thấy điểm K và H nên bạn tự làm nhé ^ ^
Cho hình vẽ bên.
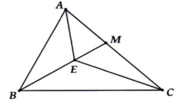
Hãy so sánh:
a) A E M ^ và A B M ^
b) A E C ^ và A B C ^
Cho hình bên, M là một điểm tùy ý nằm trên đường thẳng a. Vẽ điểm C sao cho a là đường trung trực của AC. Hãy so sánh MA + MB với BC.
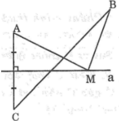
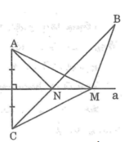
Gọi N là giao điểm của BC với đường thẳng a.
* Nếu M ≠ N
Nối MC.
Vì a là đường trung trực của AC và M ∈ a
Suy ra: MA = MC (tính chất đường trung trực) (1)
Trong ΔMBC, ta có:
BC < MB + MC (bất đẳng thức tam giác) (2)
Thay (1) vào (2) ta có: BC < MA + MB
* Nếu M trùng với N
Nối NA. Ta có:
NA = NC (tính chất đường trung trực)
Mà: MA + MB = NA + NB = NC + NB = BC
Vậy: MA + MB ≥ BC
cho hình tam giác abc có điểm n là điểm chính giữa của cạnh ac , trên hình đó có hình thang bmne như hình vẽ bên. nối b với n, nối e với m. hai đoạn thẳng này gặp nhau ở điểm o
a so sánh diện tích 2 hình tam giác obm và men
b so sánh diện tích hình tam giác emc và aemb
Trong hình 67, cung AmB có số đo là 60 ° . Hãy:
a) Vẽ góc ở tâm chắn cung AmB. Tính góc AOB.
b) Vẽ góc nội tiếp đỉnh C chắn cung AmB. Tính góc ACB.
c) Vẽ góc tạo bởi tia tiếp tuyến Bt và dây cung BA. Tính góc ABt.
d) Vẽ góc ADB có đỉnh D ở bên trong đường tròn. So sánh ADB và ACB
e) Vẽ góc AEB có đỉnh E ở bên ngoài đường tròn (E và C cùng phía đối với AB). So sánh cung AEB với cung ACB
Cho đường tròn (O;R), 2 dây cung AB và CD cắt nhau tại điểm M nằm bên trong đường tròn.
a) Cm rằng nếu AB=CD thì MA=MC
b) Trường hợp AB>CD. Hãy so sánh khoảng cách từ M đến trung điểm của các dây AB, CD (vẽ hình luôn nha)
Cho tam giác ABC, cho điểm M nằm trong tam giác. AM cắt BC tại N. a) Hãy chỉ ra góc ngoài tại đỉnh M của tam giác BMN và so sánh AMB và MNB. b) Hãy chỉ ra góc ngoài tại đỉnh M của tam giác AMC và so sánh NMC và MAC. (Huhu mấy bạn vẽ hình giúp mình nữa nhó^^) Thankssssss~~~~~
Cho tam giác ABC, cho điểm M nằm trong tam giác. AM cắt BC tại N. a) Hãy chỉ ra góc ngoài tại đỉnh M của tam giác BMN và so sánh AMB và MNB. b) Hãy chỉ ra góc ngoài tại đỉnh M của tam giác AMC và so sánh NMC và MAC. (Huhu mấy bạn vẽ hình giúp mình nữa nhó^^) Thankssssss~~~~~
Cho hình vẽ bên biết a // b và A 1 ^ + A 2 ^ + A 3 ^ = 310 ° .
a) Tính A 1 ^
b) So sánh A 2 ^ và B 4 ^

a) Ta có: A 1 ^ + A 2 ^ + A 3 ^ = 310 ° mà A 2 ^ + A 3 ^ = 180 ° ( hai góc kề bù)
do đó A 1 ^ = 310 ° − 180 ° = 130 ° .
b) Ta có: B 2 ^ = A 2 ^ (hai góc đồng vị); B 2 ^ = B 4 ^ (hai góc đối đỉnh).
Suy ra A 2 ^ = B 4 ^