Hãy tính x và y trong mỗi hình sau: (h.6)
Hình 6
Hãy tính x và y trong mỗi hình sau: (h.6)
Hình 6
Áp dụng định lí Pitago ta có:
![]()
Áp dụng định lí 3 ta có:
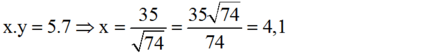
Hãy tính x và y trong mỗi hình sau: (h.7)
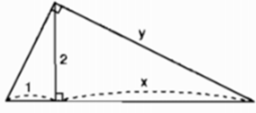
Hình 7
Theo định lí 2 ta có:
2 2 = 1 . x = > x = 4
Theo định lí 1 ta có:
y 2 = x ( 1 + x ) = 4 ( 1 + 4 ) = 20 = > y = √ 20 = 2 √ 5
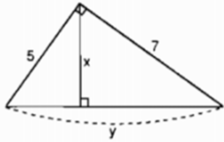
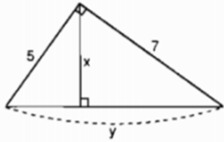
Hãy tính x và y trong mỗi hình sau: (h.5)
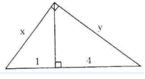
Hình 5
Hãy tính x và y trong mỗi hình sau: (h.5)
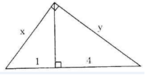
Hình 5
Hãy tính x và y trong mỗi hình sau: (h.7)
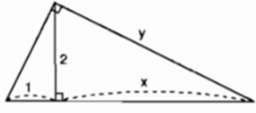
Hình 7
Theo định lí 2 ta có:
22 = 1.x => x = 4
Theo định lí 1 ta có:
y2 = x(1 + x) = 4(1 + 4) = 20
=> y = √20 = 2√5
Hãy tính x và y trong mỗi hình sau: (h.4a, b)
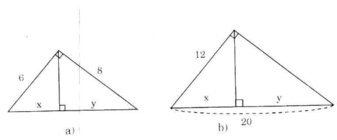
Hình 4
- Hình a
Theo định lí Pitago ta có:
![]()
Áp dụng định lí 1 ta có:
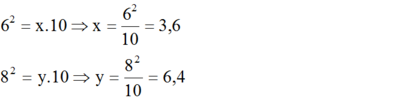
- Hình b
Áp dụng định lí 1 ta có:
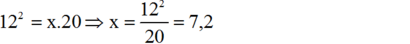
=> y = 20 - 7,2 = 12,8
Hãy tính x và y trong mỗi hình sau: (h.4a, b)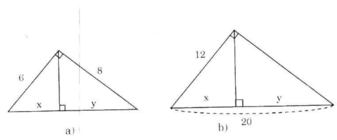
Hình 4
- Hình a
Theo định lí Pitago ta có:
![]()
Áp dụng định lí 1 ta có:
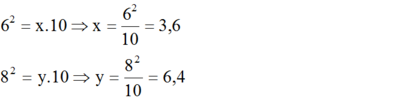
- Hình b
Áp dụng định lí 1 ta có:
![]()
=> y = 20 - 7,2 = 12,8
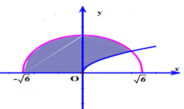
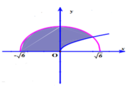
Gọi H là hình phẳng giới hạn bởi đồ thị hàm số y = x , cung tròn có phương trình y = 6 - x 2 ( - 6 ≤ x ≤ 6 ) và trục hoành (phần tô đậm trong hình vẽ bên). Tính thể tích V của vật thể tròn xoay sinh bởi khi quay hình phẳng H quanh trục
![]()
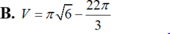
![]()
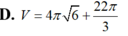
Gọi H là hình phẳng giới hạn bởi đồ thị hàm số y = x , cung tròn có phương trình y = 6 - x 2 - 6 ≤ x ≤ 6 và trục hoành (phần tô đậm trong hình vẽ bên). Tính thể tích V của vật thể tròn xoay sinh bởi khi quay hình phẳng H quanh trục
A. V = 4 π 6 + 22 π
B. V = π 6 - 22 π 3
C. V = 8 π 6 + 11 π
D. V = 4 π 6 + 22 π 3
Chọn D.
Phương pháp: Chia miền cần tính thể tích làm 2 phần.
