Tính diện tích miền gạch sọc.
Tính diện tích hình HOABINH (miền gạch sọc).
Hình 62
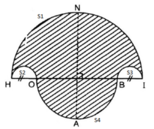
Diện tích miền gạch sọc bằng:
S = S1 – S2 – S3 + S4
với:
+ S1 là nửa đường tròn đường kính HI
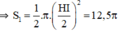
+ S2; S3 là nửa đường tròn đường kính HO và BI.
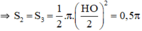
+ Ta tính OB:
Ta có: HO+ OB + BI = HI
⇔ 2+ OB + 2= 10 nên OB = 6
+ S4 là nửa đường tròn đường kính OB
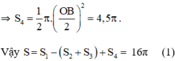
Hãy tính diện tích miền gạch sọc trong các hình 69, 70, 71 (đơn vị độ dài: cm).

* Hình c
Dựa vào hình vẽ,diện tích phần gạch sọc bằng diện tích hình vuông trừ đi bốn phần diện tích hình quạt ở bốn góc ( Mỗi hình quạt tương ứng 1/4 hình tròn bán kính 1,5 cm. Do đó, tổng 4 phần tương ứng với diện tích của một hình tròn bán kính 1,5 cm )
Hình vuông có độ dài cạnh 3 cm nên có diện tích là: S = 32 = 9 ( cm2).
Hình tròn có bán kính là R= 1,5 cm nên diện tích hình tròn là:
s= π.1,52 cm2
Diện tích phần gạch sọc là: Ssọc= S – s = 9- π.1,52≈ 1, 94 cm2
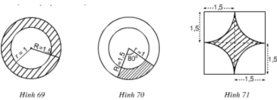
Hãy tính diện tích miền gạch sọc trong các hình 69, 70, 71 (đơn vị độ dài: cm).
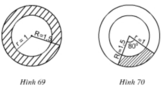
- Hình 69
Gọi R,r lần lượt là bán kính đường tròn lownsvaf đường tròn nhỏ.
Đo đạc ta được:
R=1,5cm;r=1cm
Diện tích hình tròn lớn: 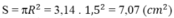
Diện tích hình tròn nhỏ: ![]()
Diện tích hình gạch sọc: ![]()
- Hình 70 Đo đạc ta được R=1,5cm;r=1cm, n = 80 o
Diện tích hình quạt lớn: ![]()
Diện tích hình quạt nhỏ: ![]()
Diện tích phần gạch sọc: ![]()
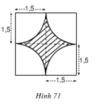
Hình 71
Dựa vào hình vẽ,diện tích phần gạch sọc bằng diện tích hình vuông trừ đi bốn phần diện tích hình quạt ở bốn góc ( Mỗi hình quạt tương ứng 1/4 hình tròn bán kính 1,5 cm. Do đó, tổng 4 phần tương ứng với diện tích của một hình tròn bán kính 1,5 cm )
Hình vuông có độ dài cạnh 3 cm nên có diện tích là: S = 32 = 9 ( cm2).
Hình tròn có bán kính là R= 1,5 cm nên diện tích hình tròn là:
s= π.1,52 cm2
Diện tích phần gạch sọc là: Ssọc= S – s = 9- π.1,52≈ 1, 94 cm2
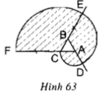
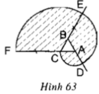
a) Vẽ lại hình tạo bởi các cung tròn xuất phát từ đỉnh C của tam giác đều ABC cạnh 1cm. Nêu cách vẽ (h.63).
b) Tính diện tích miền gạch sọc.

Kiến thức áp dụng
Diện tích hình quạt tròn bán kính R, cung nº được tính theo công thức:
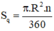
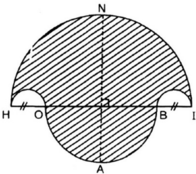
a) Vẽ hình 62 (tạo bởi các cung tròn) với HI = 10cm và HO = BI = 2cm. Nêu cách vẽ.
b) Tính diện tích hình HOABINH (miền gạch sọc).
c) Chứng tỏ rằng hình tròn đường kính NA có cùng diện tích với hình HOABINH đó .
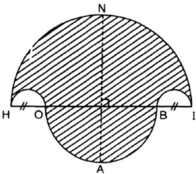
Hình 62
a) Cách vẽ
- Vẽ nửa đường tròn đường kính HI = 10cm, tâm M.
- Trên đường kính HI lấy điểm O và điểm B sao cho HO = BI = 2cm.
- Vẽ hai nửa đường tròn đường kính HO, BI nằm cùng phía với đường tròn (M).
- Vẽ nửa đường tròn đường kính OB nằm khác phía đối với đường tròn (M). Đường thẳng vuông góc với HI tại M cắt (M) tại N và cắt đường tròn đường kính OB tại A.
b)
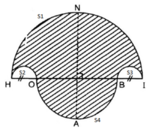
Diện tích miền gạch sọc bằng:
S = S 1 − S 2 − S 3 + S 4
với:
+ S 1 là nửa đường tròn đường kính HI
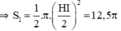
+ S 2 ; S 3 là nửa đường tròn đường kính HO và BI.
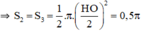
+ Ta tính OB:
Ta có: HO+ OB + BI = HI
⇔ 2+ OB + 2= 10 nên OB = 6
+ S4 là nửa đường tròn đường kính OB
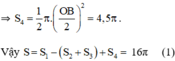
c)Ta có: 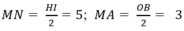
Do đó, NA = MN+ MA= 8
Diện tích hình tròn đường kính NA bằng : π 4 2 = 16 π ( c m 2 ) ( 2 )
so sánh (1) và (2) ta thấy hình tròn đường kính NA có cùng diện tích với hình HOABINH.
tính diện tích phần gạch sọc trong hình vẽ sau
Tính diện tích phần đã gạch sọc của hình chữ nhật, theo hình vẽ sau :

Biết đáy bé hình thang là 10,6cm . Đáy lớn hình thang là 15,9cm . Tính diện tích phần gạch sọc .
Tính diện tích phần gạch sọc. Biết cạnh hình vuông là 8cm. Trả lời:…………………

làm nhanh giúp mik
11/1 lúc 16:00 mik phải nộp rồi
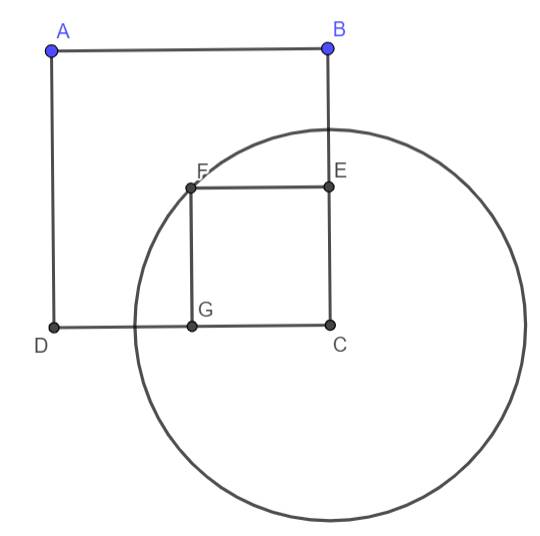
Diện tích của phần gạch sọc là diện tích của \(8\) hình lá nhỏ.
Diện tích \(2\) hình lá nhỏ (mô tả như hình vẽ trên) là hiệu của \(\dfrac{1}{4}\) diện tích hình tròn trừ đi diện tích hình vuông \(CEFG\).
Do đó diện tích của \(8\) hình lá nhỏ (tức diện tích phần gạch sọc) là diện tích của hình tròn trừ đi diện tích hình vuông \(ABCD\).
Diện tích hình tròn là: \(S_1=3,14\times CF\times CF=3,14\times\dfrac{CA}{2}\times\dfrac{CA}{2}=0,785\times CA\times CA\)
Diện tích hình vuông \(ABCD\) là: \(S_2=8\times8=64\left(cm^2\right)\)
Mà ta cũng có thể tính diện tích hình vuông \(ABCD\) bằng cách:
\(S_2=\dfrac{AC\times BD}{2}=\dfrac{AC\times AC}{2}\)
Suy ra \(AC\times AC=64\times2=128\)
Diện tích phần gạch sọc là:
\(S_1-S_2=0,785\times AC\times AC-\dfrac{AC\times AC}{2}=0,285\times AC\times AC=36,48\left(cm^2\right)\)