Tính đạo hàm của hàm số sau: 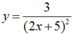
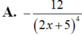
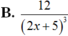
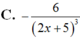
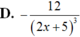
Tính đạo hàm của các hàm số sau:
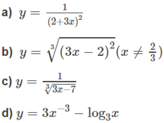
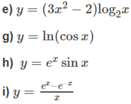
Tính đạo hàm của hàm số sau y = sin cos 2 x . tan 2 x
A. y ' = cos cos 2 x . tan 2 x − sin 2 x tan 2 x + 2 tan x
B. y ' = cos cos 2 x . tan 2 x sin 2 x tan 2 x + tan x
C. y ' = cos cos 2 x . tan 2 x − sin 2 x tan 2 x + tan x
D. y ' = cos cos 2 x . tan 2 x sin 2 x tan 2 x + 2 tan x
Chọn A
Áp dụng sin u / , với u = cos 2 x tan 2 x
y ' = cos cos 2 x . tan 2 x . cos 2 x . tan 2 x / .
Tính cos 2 x . tan 2 x / , bước đầu sử dụng u . v / , sau đó sử dụng u α / .
cos 2 x . tan 2 x / = cos 2 x / . tan 2 x + tan 2 x / . cos 2 x
= 2 cos x cos x / tan 2 x + 2 tan x tan x / cos 2 x
= − 2 sin x cos x tan 2 x + 2 tan x 1 cos 2 x cos 2 x = − sin 2 x tan 2 x + 2 tan x .
Vậy y ' = cos cos 2 x . tan 2 x − sin 2 x tan 2 x + 2 tan x
Tính đạo hàm của hàm số sau y = sin 2 cos tan 4 3 x
A. y ' = sin 2 cos tan 4 3 x . sin tan 4 3 x .4 tan 3 3 x . 1 + tan 2 3 x .3
B. y ' = sin 2 cos tan 4 3 x . sin tan 4 3 x . tan 3 3 x . 1 + tan 3 3 x .
C. y ' = − sin 2 cos tan 4 3 x . sin tan 4 3 x .4 tan 3 3 x . 1 + tan 2 3 x .3
D. y ' = sin 2 cos tan 4 3 x . sin tan 4 3 x .4 tan 3 3 x
Chọn C
Đầu tiên áp dụng u α / , với u = sin cos tan 4 3 x
y ' = 2 sin cos tan 4 3 x . sin cos tan 4 3 x /
Sau đó áp dụng sin u / , với u = cos tan 4 3 x
y ' = 2 sin cos tan 4 3 x . cos cos tan 4 3 x . cos tan 4 3 x /
Áp dụng cos u / , với u = tan 4 3 x .
y ' = − sin 2 cos tan 4 3 x . sin tan 4 3 x . tan 4 3 x / .
Áp dụng u α / , với u = tan 3 x
y ' = − sin 2 cos tan 4 3 x . sin tan 4 3 x .4 tan 3 3 x . tan 3 x / .
y ' = − sin 2 cos tan 4 3 x . sin tan 4 3 x .4 tan 3 3 x . 1 + tan 2 3 x . 3 x / .
y ' = − sin 2 cos tan 4 3 x . sin tan 4 3 x .4 tan 3 3 x . 1 + tan 3 3 x .3
Tính đạo hàm của hàm số sau: y = sin 3 2 x + 1 .
A. sin 2 2 x + 1 cos 2 x + 1 .
B. 12 sin 2 2 x + 1 cos 2 x + 1 .
C. 3 sin 2 2 x + 1 cos 2 x + 1 .
D. 6 sin 2 2 x + 1 cos 2 x + 1 .
Chọn D
Bước đầu tiên áp dung công thức u α / với u = sin 2 x + 1
Vậy
y ' = sin 3 2 x + 1 / = 3 sin 2 2 x + 1 . sin 2 x + 1 / .
* Tính sin 2 x + 1 / : Áp dụng sin u / , với u = 2 x + 1
Ta được:
sin 2 x + 1 / = cos 2 x + 1 . 2 x + 1 / = 2 cos 2 x + 1 .
⇒ y ' = 3. sin 2 2 x + 1 .2 cos 2 x + 1 = 6 sin 2 2 x + 1 cos 2 x + 1 .
Tính đạo hàm của hàm số sau y = sin x 1 + cos x 3
A. sin 2 x 1 + cos x 3
B. 3 sin 2 x 1 + cos x 2
C. 2 sin 2 x 1 + cos x 2
D. 3 sin 2 x 1 + cos x 3
Chọn D.
Bước đầu tiên ta áp dụng công thức u α / với u = sin x 1 + cos x
y ' = 3 sin x 1 + cos x 2 . sin 1 + cos x /
Tính :
sin x 1 + cos x / = sin x / 1 + cos x − 1 + cos x / . sin x 1 + cos x 2 = cos x 1 + cos x + sin 2 x 1 + cos x 2
= cos x + cos 2 x + sin 2 x 1 + cos x 2 = cosx + 1 ( 1 + c osx) 2 = 1 1 + cos x .
Vậy
y ' = 3 sin x 1 + cos x 2 . 1 1 + cos x = 3 sin 2 x 1 + cos x 3
Tính đạo hàm của hàm số sau y = tan x + cot x
A. 1 cos 2 x + cot 2 x
B. tan 2 x + cot 2 x + 1
C. 1 cos 2 x + 1 sin 2 x
D. 1 cos 2 x − 1 sin 2 x
y = tan x + cot x ⇒ y ' = ( tan x + cot x ) ' = ( tan x ) ' + ( cot x ) ' = 1 cos 2 x − 1 sin 2 x
Chọn đáp án D
Tính đạo hàm của hàm số sau: f x = ln x 2 + 1
A. f ' ( x ) = ln ( x 2 + 1 )
B. f ' x = ln 2 x
C. f ' x = 1 x 2 + 1
D. f ' x = 2 x x 2 + 1
Đáp án D
Phương pháp:
Công thức tính đạo hàm hàm hợp: f ; u x = u ' x . f ' u .
Công thức tính đạo hàm: ln u ' = u ' u
Cách giải:
Có: f x = ln x 2 + 1 ⇒ f ' x = x 2 + 1 ' x 2 + 1 = 2 x x 2 + 1
Chú ý khi giải: HS thường nhầm lẫn: sử dụng công thức tính đạo hàm ln x ' = 1 x mà không chú ý đến công thức tính đạo hàm hàm hợp.
Tính đạo hàm của hàm số sau: y = 2 s i n 2 4 x - 3 c o s 3 5 x .
A. y ' = sin 8 x + 45 2 cos 5 x . sin 10 x
B. y ' = 8 sin 8 x + 5 2 cos 5 x . sin 10 x
C. y ' = 8 sin 8 x + 45 2 cos 5 x . sin 10 x
D. y ' = - 8 sin 8 x + 45 2 cos 5 x . sin 10 x
- Bước đầu tiên áp dụng (u - v)'.
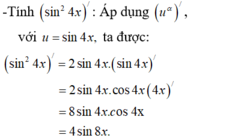
- Tương tự:
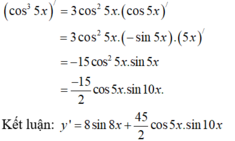
Chọn C
Tính đạo hàm của hàm số sau y = sin x sin x - cos x
A. y ' = - 1 sin x + cos x 2
B. y ' = 1 sin x - cos x 2
C. y ' = 1 sin x + cos x 2
D. y ' = - 1 sin x - cos x 2