Diện tích hình phẳng giới hạn bởi các đồ thị hàm số (H) : y = x 3 - 3 x 2 + 3 x - 1 y = 1 - x x = 0 , x = 2
A. 1
B. 3 2
C. 2
D. 3
Những câu hỏi liên quan
Cho hình phẳng giới hạn bởi đồ thị các hàm số
y
x
, đường thẳng y 2 - x và trục hoành. Diện tích hình phẳng sinh bởi hình phẳng giới hạn bởi các đồ thị trên là A.
7
6
.
B.
4
3
.
C.
5
6
.
D.
5
4
.
Đọc tiếp
Cho hình phẳng giới hạn bởi đồ thị các hàm số y = x , đường thẳng y = 2 - x và trục hoành. Diện tích hình phẳng sinh bởi hình phẳng giới hạn bởi các đồ thị trên là
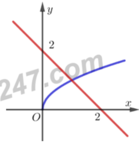
A. 7 6 .
B. 4 3 .
C. 5 6 .
D. 5 4 .
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số x 3 - x và đồ thị hàm số y = x - x 2
A. 9 4
B. 37 12
C. 81 12
D. 13
Tìm hoành độ các giao điểm của hai đồ thị, ta có:
x 3 - x = x - x 3 <=> x 3 + x 2 - 2 x = 0
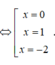
Vậy diện tích của hình phẳng tính là
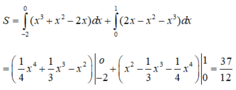
Vậy chọn đáp án B.
Đúng 0
Bình luận (0)
Hình phẳng (H) được giới hạn bởi đồ thị hai hàm số
y
x
2
-
1
,
y
x
+
5
. Diện tích của (H) bằng A.
71
3
B.
73
3
C.
70
3
D.
74...
Đọc tiếp
Hình phẳng (H) được giới hạn bởi đồ thị hai hàm số y = x 2 - 1 , y = x + 5 . Diện tích của (H) bằng
A. 71 3
B. 73 3
C. 70 3
D. 74 3
Chọn B.
Xét pt x 2 - 1 = x + 5 có nghiệm x= -3, x = 3
Suy ra
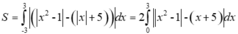
Bảng xét dấu x 2 - 1 trên đoạn [0; 3]
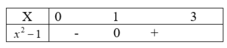
Vậy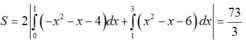 
Đúng 0
Bình luận (0)
Cho hình phẳng (H) giới hạn bởi đồ thị hàm số
y
x
−
1
x
+
2
và các đường thẳng
Δ
:
y
2
,
d
:
−
2
x
−
4
(tham khảo hình bên). Tính diện tích hình phẳng (H) A.
1...
Đọc tiếp
Cho hình phẳng (H) giới hạn bởi đồ thị hàm số y = x − 1 x + 2 và các đường thẳng Δ : y = 2 , d : − 2 x − 4 (tham khảo hình bên). Tính diện tích hình phẳng (H)
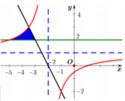
A. 1 4 + 3 ln 2
B. 1 4
C. − 2 + 3 ln 3
D. − 5 4 + 3 ln 2
Đáp án D
Hoành độ giao điểm của (H) và (d) là nghiệm: x − 1 x + 2 = − 2 x − 4 ⇔ x = − 1 x = − 7 2
Hoành độ giao điểm của (d) và Δ là nghiệm: 2 = − 2 x − 4 ⇔ x = − 3
Hoành độ giao điểm của (H) và Δ là nghiệm: x − 1 x + 2 = 2 ⇔ x = − 5
Khi đó, diện tích hình phẳng cần tính là S = ∫ − 5 − 7 2 x − 1 x + 2 − 2 d x + ∫ − 7 2 − 3 − 2 x − 4 − 2 d x = − 5 4 + 3 ln 2
Đúng 0
Bình luận (0)
Diện tích hình phẳng giới hạn bởi các đồ thị hàm số y cosx, y sinx , đường thẳng
x
π
2
;
x
3
π
2
. A.
3
B.
2
2
C.
2
D. 1.
Đọc tiếp
Diện tích hình phẳng giới hạn bởi các đồ thị hàm số y = cosx, y = sinx , đường thẳng x = π 2 ; x = 3 π 2 .
A. 3
B. 2 2
C. 2
D. 1.
Chọn B.
Đặt f1(x) = cosx, f2(x) =sinx ;
Ta có f1(x) - f2(x) = 0 <=> cosx - sinx = 0 <=> x = 5 π 4 ∈ π 2 ; 3 π 2
Diện tích hình phẳng đã cho là:
Đúng 0
Bình luận (0)
Cho hình (H) là hình phẳng giới hạn bởi 2 đồ thị của 2 hàm số
y
x
2
và y x+2 Diện tích của hình (H) bằng A. 7/6 B. -9/2 C. 3/2 D. 9/2
Đọc tiếp
Cho hình (H) là hình phẳng giới hạn bởi 2 đồ thị của 2 hàm số y = x 2 và y = x+2 Diện tích của hình (H) bằng
A. 7/6
B. -9/2
C. 3/2
D. 9/2
Cho hình (H) là hình phẳng giới hạn bởi 2 đồ thị của 2 hàm số y = x2 và y = x+2. Diện tích của hình (H) bằng
A. 7/6
B. - 9/2
C. 3/2
D. 9/2
Đáp án D
Phương pháp:
Diện tích hình phẳng tạo bởi hai đồ thị hàm số y = f(x), y = g(x) và các đường thẳng x = a, x = b, a<b
Cách giải: Phương trình hoành độ giao điểm của y = x2 và y = x+2
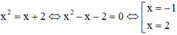
Diện tích hình (H):
Đúng 0
Bình luận (0)
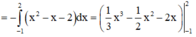
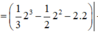
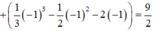
Tính diện tích hình phẳng giới hạn bởi đồ thị các hàm số y = e x ; y = 2 và đường thẳng x =1
A.e-2
B.2ln2-4
C.e+2ln2
D.e+2ln2-4
Chọn D.
Giải PT : e x = 2 ⇔ x = ln 2 Diện tích hình phẳng cần tìm là :
Đúng 0
Bình luận (0)
Gọi S là diện tích hình phẳng giới hạn bởi các đồ thị hàm số:
y
x
3
-
3
x
;
y
x
. Tính S ? A.
S
4
B.
S
8
C.
S
2
.
D.
S
0
Đọc tiếp
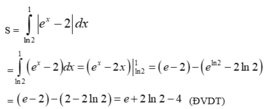
Gọi S là diện tích hình phẳng giới hạn bởi các đồ thị hàm số: y = x 3 - 3 x ; y = x . Tính S ?
A. S = 4
B. S = 8
C. S = 2 .
D. S = 0
