Có bao nhiêu giá trị của x thỏa mãn: x^3-x^2+=0
Có bao nhiêu giá trị của x thỏa mãn (|x|+2)(6−2|x|)=0?
A. 4
B. 1
C. 2
D. 3
Có bao nhiêu giá trị x ∈Z thỏa mãn |x + 2| + (-7) = -3
A. 0
B. 1
C. 3
D. 2
Có bao nhiêu giá trị của x thỏa mãn ( x + 5 ) 2 – 2 ( x + 5 ) ( x – 2 ) + ( x – 2 ) 2 = 49
A. 1
B. 2
C. 3
D. Vô số
( x + 5 ) 2 – 2 ( x + 5 ) ( x – 2 ) + ( x – 2 ) 2 = 49 ⇔ ( ( x + 5 ) – ( x – 2 ) ) 2 = 49 ⇔ ( x + 5 – x + 2 ) 2 = 49 ⇔ 7 2 = 49
Vậy với mọi x đều thỏa mãn
Đáp án cần chọn là: D
Có bao nhiêu giá trị x thỏa mãn ( 2 x + 1 ) 2 – 4 ( x + 3 ) 2 = 0
A. 0
B. 1
C. 2
D. 3
Ta có
( 2 x + 1 ) 2 – 4 ( x + 3 ) 2 = 0 ⇔ 2 x 2 + 2.2 x .1 + 1 2 − 4 x 2 + 6 x + 9 = 0 ⇔ 4 x 2 + 4 x + 1 – 4 x 2 – 24 x – 36 = 0 ⇔ - 20 x = 35 ⇔ x = - 7 4
Vậy có một giá trị của x thỏa mãn yêu cầu.
Đáp án cần chọn là: B
Có bao nhiêu giá trị x nguyên dương thỏa mãn (x - 3).(x + 2) = 0 là:
A. 3
B. 2
C. 0
D. 1
Có bao nhiêu giá trị x thỏa mãn 2 ( x + 3 ) – x 2 – 3 x = 0
A. 0
B. 2
C. 1
D. 3
2 ( x + 3 ) – x 2 – 3 x = 0 ⇔ 2 ( x + 3 ) – x 2 – 3 x = 0 ⇔ 2 ( x + 3 ) – ( x 2 + 3 x ) = 0
ó 2(x + 3) – x(x + 3) = 0
ó (2 – x)(x + 3) = 0
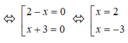
Vậy có hai giá trị x thỏa mãn
Đáp án cần chọn là: B
Có bao nhiêu giá trị nguyên dương thỏa mãn (x - 3).(x + 2) = 0
Có bao nhiêu giá trị của x thỏa mãn 2 x 3 (2x – 3) – x 2 (4x2 – 6x + 2) = 0
A. 2
B. 3
C. 0
D. 1
2 x 3 ( 2 x – 3 ) – x 2 ( 4 x 2 – 6 x + 2 ) = 0 ⇔ 4 x 4 – 6 x 3 – 4 x 4 + 6 x 3 – 2 x 2 = 0 ⇔ - 2 x 2 = 0
ó x = 0
Vậy x = 0
Có 1 giá trị của x thỏa mãn đề bài
Đáp án cần chọn là: D
Có bao nhiêu giá trị nguyên của tham số m ∈ [ -2020; 2020 ] thỏa mãn phương trình : \(x^2+\left(2-m\right)x+1=2\sqrt{x^3+x}\) có nghiệm ?
ĐKXĐ: \(x\ge0\)
\(x^2+1+\left(2-m\right)x-2\sqrt{x\left(x^2+1\right)}=0\)
Với \(x=0\) ko phải nghiệm, với \(x>0\) chia 2 vế cho x:
\(\Rightarrow\dfrac{x^2+1}{x}+2-m-2\sqrt{\dfrac{x^2+1}{x}}=0\)
Đặt \(\sqrt{\dfrac{x^2+1}{x}}=t\ge\sqrt{2}\)
\(\Rightarrow t^2-2t+2=m\)
Xét hàm \(f\left(t\right)=t^2-2t+m\) khi \(t\ge\sqrt{2}\)
\(\left\{{}\begin{matrix}a=1>0\\-\dfrac{b}{2a}=1< \sqrt{2}\end{matrix}\right.\) \(\Rightarrow f\left(t\right)\) đồng biến khi \(t\ge\sqrt{2}\)
\(\Rightarrow f\left(t\right)\ge f\left(\sqrt{2}\right)=4-2\sqrt{2}\)
\(\Rightarrow\) Pt có nghiệm khi \(m\ge4-2\sqrt{2}\)
