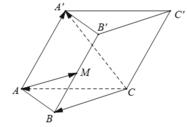
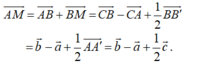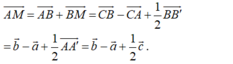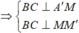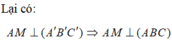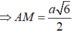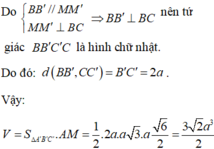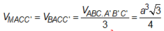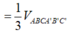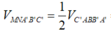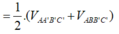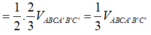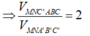Cho hình lăng trụ ABC.A'B'C', M là trung điểm của BB’. Đặt C A → = a → , C B → = b → , A A ' → = c → . Biểu diễn A M → theo các vecto a → , b → , c → .

Những câu hỏi liên quan
Cho hình lăng trụ ABC.ABC, M là trung điểm của BB’. Đặt
C
A
→
a
→
,
C
B
→
b
→
,
A
A
→
c
→
. Khẳng định nào sau đây đúng? A.
A
M...
Đọc tiếp
Cho hình lăng trụ ABC.A'B'C', M là trung điểm của BB’. Đặt C A → = a → , C B → = b → , A A ' → = c → . Khẳng định nào sau đây đúng?
A. A M → = b → + c → - 1 2 a →
B. A M → = a → - c → + 1 2 b →
C. A M → = a → + c → - 1 2 b →
D. A M → = b → - a → + 1 2 c →
Phần I: Trắc nghiệmCho hình lăng trụ ABC.ABC, M là trung điểm của BB’. Đặt
C
A
→
a
→
,
C
B
→
b
→
,
A
A
→
c
→
. Khẳng định nào sau đây đúng? A.
A...
Đọc tiếp
Phần I: Trắc nghiệm
Cho hình lăng trụ ABC.A'B'C', M là trung điểm của BB’. Đặt C A → = a → , C B → = b → , A ' A → = c → . Khẳng định nào sau đây đúng?
A. A M → = b → + c → - 1 2 a →
B. A M → = a → - c → + 1 2 b →
C. A M → = a → + c → - 1 2 b →
D. A M → = b → - a → + 1 2 c →
Cho khối lăng trụ ABC.ABC, hình chiếu của điểm A lên mặt phẳng (ABC) là trung điểm M của cạnh BC và
A
M
a
3
, hình chiếu của điểm A lên mặt phẳng (BCCB) là H sao cho MH song song với BB và AHa , khoảng cách giữa hai đường thẳng BB, CC bằng 2a. Thể tích khối lăng trụ đã cho là A.
3
a
3
2
B.
a
3...
Đọc tiếp
Cho khối lăng trụ ABC.A'B'C', hình chiếu của điểm A lên mặt phẳng (A'B'C') là trung điểm M của cạnh B'C' và A ' M = a 3 , hình chiếu của điểm A lên mặt phẳng (BCC'B') là H sao cho MH song song với BB' và AH=a , khoảng cách giữa hai đường thẳng BB', CC' bằng 2a. Thể tích khối lăng trụ đã cho là
A. 3 a 3 2
B. a 3 2
C. 2 a 3 2 3
D. 3 a 3 2 2
Cho hình lăng trụ đứng ABC.ABC có đáy ABC là tam giác cân tại C, BAC 30
°
, AB a
3
, AA a. Gọi M là trung điểm của BB. Tính theo a thể tích V của khối tứ diện MACC. A. V
a
3
3
12
B. V
a
3
3
4
C....
Đọc tiếp
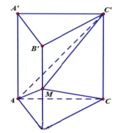
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác cân tại C, BAC = 30 ° , AB = a 3 , AA' = a. Gọi M là trung điểm của BB'. Tính theo a thể tích V của khối tứ diện MACC'.
A. V = a 3 3 12
B. V = a 3 3 4
C. V = a 3 3 3
D. V = a 3 3 18
Cho hình lăng trụ đứng ABC.ABC có đáy ABC là tam giác cân tại C, AAa,
B
A
C
^
30
0
,
A
B
a
3
. Gọi M là trung điểm của BB. Tính theo a thể tích V của khối tứ diện MACC A.
V
a
3
3...
Đọc tiếp
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác cân tại C, AA'=a, B A C ^ = 30 0 , A B = a 3 . Gọi M là trung điểm của BB'. Tính theo a thể tích V của khối tứ diện MACC'
A. V = a 3 3 12
B. V = a 3 3 4
C. V = a 3 3 3
D. V = a 3 3 18
Cho khối lăng trụ ABC.ABC, hình chiếu của điểm A lên mặt phẳng (ABC) là trung điểm M của cạnh BC và AMa
3
, hình chiếu của điểm A lên mặt phẳng (BCCB) là H sao cho MH song song với BB và AHa, khoảng cách giữa hai đường thẳng BB , CC bằng 2a . Thể tích khối lăng trụ đã cho là A.
3
2
a
3
B.
2...
Đọc tiếp
Cho khối lăng trụ ABC.A'B'C', hình chiếu của điểm A lên mặt phẳng (A'B'C') là trung điểm M của cạnh B'C' và A'M=a 3 , hình chiếu của điểm A lên mặt phẳng (BCC'B') là H sao cho MH song song với BB' và AH=a, khoảng cách giữa hai đường thẳng BB' , CC' bằng 2a . Thể tích khối lăng trụ đã cho là
A. 3 2 a 3
B. 2 a 3
C. 2 2 a 3 3
D. 3 2 a 3 2
Chọn D
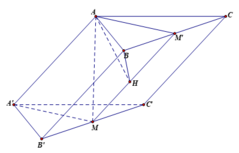
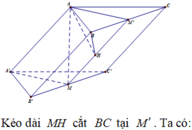
Kéo dài MH cắt BC tại M'. Ta có
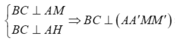
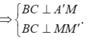
Tại có:
![]()
![]()
nên tam giác AMM' vuông tại A
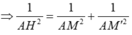
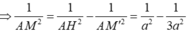
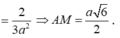
Do
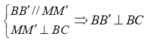
nên tứ giác BB'C'C là hình chữ nhật.
Do đó:
![]()
![]()
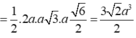
Đúng 0
Bình luận (0)
Cho hình lăng trụ ABC.ABC Gọi M, N lần lượt là trung điểm của AA’, BB’. Tính tỉ số
V
M
N
C
A
B
C
V
M
N
A
B
C
A. 2 B. 1,5 C. 2,5 D. 3
Đọc tiếp
Cho hình lăng trụ ABC.A'B'C' Gọi M, N lần lượt là trung điểm của AA’, BB’. Tính tỉ số V M N C ' A B C V M N A ' B ' C '
A. 2
B. 1,5
C. 2,5
D. 3
Đáp án A
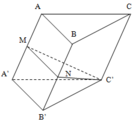
V A A ' B ' C ' = V C ' A B C = V A B B ' C ' = 1 3 V A B C A ' B ' C ' V M N A ' B ' C ' = 1 2 V C ' A B B ' A ' = 1 2 . ( V A A ' B ' C ' + V A B B ' C ' ) = 1 2 . 2 3 V A B C A ' B ' C ' = 1 3 V A B C A ' B ' C ' ⇒ V M N C ' A B C V M N A ' B ' C ' = 2
Đúng 0
Bình luận (0)
Cho hình lăng trụ ABC.ABC. Gọi M, N lần lượt là trung điểm của AA’, BB’. Tính tỉ số
V
M
N
C
A
B
C
V
M
N
A
B
C...
Đọc tiếp
Cho hình lăng trụ ABC.A'B'C'. Gọi M, N lần lượt là trung điểm của AA’, BB’. Tính tỉ số V M N C ' A B C V M N A ' B ' C '
A. 2
B. 1,5
C. 2,5
D. 3
Cho hình lăng trụ đứng ABC.ABC có đáy ABC là tam giác cân tại C, AB 2a, AAa , góc giữa BC và (ABBA) bằng
60
o
. Gọi N là trung điểm AA và M là trung điểm BB. Tính khoảng cách từ điểm M đến mặt phẳng (BCN). A.
2
a
74
37...
Đọc tiếp
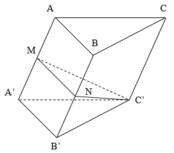
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác cân tại C, AB = 2a, AA'=a , góc giữa BC' và (ABB'A') bằng 60 o . Gọi N là trung điểm AA' và M là trung điểm BB'. Tính khoảng cách từ điểm M đến mặt phẳng (BC'N).
A. 2 a 74 37
B. a 74 37
C. 2 a 37 37
D. a 37 37
Chọn A
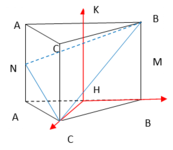
Gọi H, K lần lượt là là trung điểm cạnh A'B' và AB. Từ giả thiết ta có
![]()
![]()
Mặt khác: HC', HB' và HK đôi một vuông góc nhau.
Tọa độ hóa
![]()
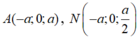
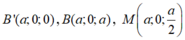
Xét mặt phẳng (BC'N) có
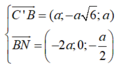
![]()
Phương trình (BC'N) là:
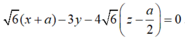
Khoảng cách từ M đến (BC'N) là:
![]()
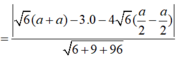

Đúng 0
Bình luận (0)