Cho hàm số y = f ( x ) có đồ thị như hình vẽ
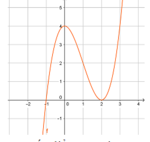
Đồ thị hàm số y = f ( x ) có mấy điểm cực trị?
A. 2
B. 1.
C. 0
D. 3
Cho đồ thị hàm số y = f(x) có đồ thị đạo hàm như hình vẽ. Số điểm cực trị của đồ thị hàm số y = f ( x 3 ) là:
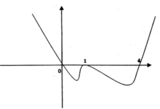
A. 0
B. 1
C. 2
D. 3
Cho hàm số y=f(x) có đồ thị như hình vẽ: Đồ thị hàm số y=f(x) có mấy điểm cực trị?
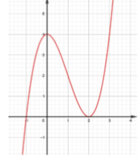
A. 0
B. 2
C. 1
D. 3
Cho hàm số y=f(x) có đồ thị như hình vẽ:
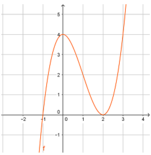
Đồ thị hàm số y=f(x) có mấy điểm cực trị?
A. 3.
B. 1.
C. 0.
D. 2.
Cho hàm số y = f ( x ) có đồ thị như hình vẽ: Đồ thị hàm số y = f ( x ) có mấy điểm cực trị?
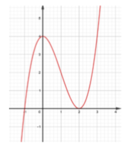
A. 0
B. 2
C. 1
D. 3
Chọn B.
Phương pháp:
Dựa vào đồ thị hàm số xác định số điểm cực trị của hàm số.
Cách giải:
Đồ thị hàm số y = f(x) có 2 điểm cực trị.
Cho hàm số y = f(x) có đồ thị như hình vẽ:
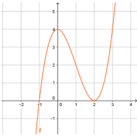
Đồ thị hàm số y = f(x) có mấy điểm cực trị?
A. 0.
B. 2.
C. 1.
D. 3
Đáp án là B
Nhìn vào đồ thị trên ta thấy đồ thị hàm số có điểm cực đại có tọa độ (0;4) và điểm cực tiểu có tọa độ (2;0), nên đồ thị hàm số trên có 2 điểm cực trị.
Cho hàm số y = f(x) có đồ thị như hình vẽ:
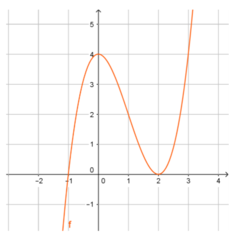
Đồ thị hàm số y = f(x) có mấy điểm cực trị?
A. 2
B. 1
C. 0
D. 3
Chọn A
Dựa vào đồ thị hàm số, ta thấy hàm số đạt cực đại tại x = 0, hàm số đạt cực tiểu tại x = 2.
Vậy đồ thị hàm số có 2 điểm cực trị.
Chọn D
Cho hàm số y = f(x) và y = g(x) có đồ thị lần lượt như hình vẽ
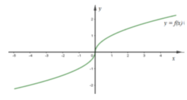
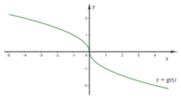
Đồ thị hàm số y = f(x).g(x) là đồ thị nào dưới đây?
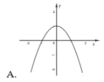
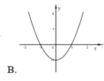
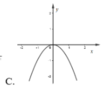
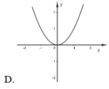
Đáp án C.
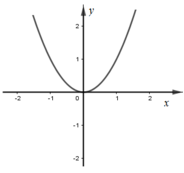
Cách giải:
Đặt y = f(x).g(x) = h(x). Khi đó:
h(0) = f(0).g(0) = 0.0 = 0
h(1) = f(1).g(1) = 1.(-1) = -1
Do đó, ta chọn phương án C
Cho hàm số y =f(x) có đạo hàm f '(x) trên tập số thực ℝ và đồ thị của hàm số y = f(x) như hình vẽ. Khi đó, đồ thị của hàm số y = f x 2 có
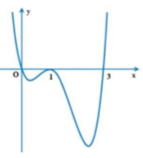
A. 2 điểm cực đại, 2 điểm cực tiểu
B. 2 điểm cực tiểu, 3 điểm cực đại
C. 1 điểm cực đại, 3 điểm cực tiểu
D. 2 điểm cực đại, 3 điểm cực tiểu
Cho hàm số y = f(x) có đạo hàm f'(x) trên khoảng
(
-
∞
;
+
∞
)
. Đồ thị hàm số y = f(x) như hình vẽ 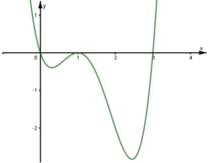
Đồ thị của hàm số y = ( f ( x ) ) 2 có bao nhiêu điểm cực đại, cực tiểu?
A. 2 điểm cực đại, 3 điểm cực tiểu.
B. 1 điểm cực đại, 3 điểm cực tiểu.
C. 2 điểm cực đại, 2 điểm cực tiểu.
A. 3 điểm cực đại, 2 điểm cực tiểu.