Nghịch đảo của số phức z = 1 - 2i là
A. 2i - 1
B. -1 -2i
C. 1 5 - 2 5 i
D. 1 5 + 2 5 i
Những câu hỏi liên quan
Cho số phức z thỏa mãn ( 2 + i ) z + 2 ( 1 + 2 i ) 1 + i . Môđun của số phức w = z + i + 1 là
A. 3
B. 4
C. 5
D. 6
Phần thực và phần ảo của số phức z thỏa mãn z = ( 1 + 2 i ) 2 + ( 1 - 2 i ) 3 là
A. 14 và 6i
B. –14 và 6
C. 14 và – 6
D. –14 và –6
Ta có:
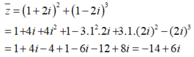
Suy ra z = -14 - 6i. Vậy phần thực và phần ảo của z là: -14 và - 6
Chọn D
Đúng 0
Bình luận (0)
Cho số phức z thỏa mãn (3 + 2i)z + (2 - i)2 = 4 + i. Môđun của số phức w = ( z + 1 ) z là
A. 2
B. 4
C. 10
D. 10
Số phức z thỏa mãn z(1 + 2i) + 1 - i = 2i là
A. -1+i
B. 1-i
C. 1+i
D. -1-i
Ta có:z(1 + 2i) + 1 - i = 2i là <=> z(1 + 2i) = -1 + 3i
Do đó:
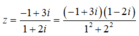
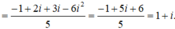
Chọn đáp án C.
Đúng 0
Bình luận (0)
Nghịch đảo của số phức z = 1 + i là
A. 1-i
B. -1+i
C. 1 2 + 1 2 i
D. 1 2 - 1 2 i
Nghịch đảo của số phức z = 1 + i là
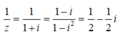
Chọn D
Đúng 0
Bình luận (0)
Cho các số phức
z
1
-
1
+
i
,
z
2
1
-
2
i
,
z
3
1
+
2
i
.
Giá trị của biểu thức
T
|
z
1
z...
Đọc tiếp
Cho các số phức z 1 = - 1 + i , z 2 = 1 - 2 i , z 3 = 1 + 2 i . Giá trị của biểu thức T = | z 1 z 2 + z 2 z 3 + z 3 z 1 | là
A. 1
B. 13
C. 5
D. 13
Cho số phức z thỏa mãn ( 1 + 2 i ) 2 . z + z = 4 i - 20 . Môđun của z là
A. 4
B. 5
C. 6
D. 10
Đặt a + bi(a, b ∈R). Ta có:
( 1 + 2 i ) 2 z = ( 1 + 2 i - 4 ) ( a + b i ) = - 3 a - 3 b i + 4 a i - 4 b = - 3 a - 4 b + ( 4 a - 3 b ) i
Do đó: ( 1 + 2 i ) 2 . z + a = 4 i - 20 <=> -3a - 4b + (4a - 3b)i + a - bi = 4i - 20
<=> -2a - 4b + (4a - 4b)i = 4i - 20
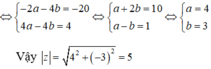
Chọn B
Đúng 0
Bình luận (0)
Tích của hai số phức z 1 = - 5 + 6 i , z 2 = 1 - 2 i là:
A. - 5 - 12i
B. 7 + 16i
C. -5 + 12i
D. 7 - 16i
Cho A và B là các điểm biểu diễn các số phức z 1 = 1 + 2 i và z 2 = 1 - 2 i . Diện tích của tam giác OAB bằng
A. 1
B. 2
C. 4
D. 5 2
