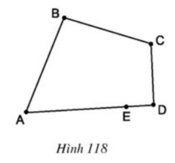
Tại sao hình gồm năm đoạn thẳng AB, BC, CD, DE, EA ở hình 118 không phải là đa giác?
Những câu hỏi liên quan
Xem hình 10
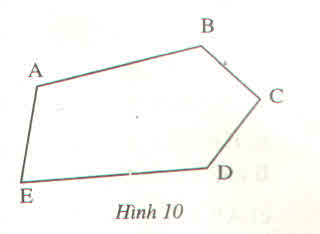
a) Đo rồi sắp xếp độ dài các đoạn thẳng AB, BC, CD, DE, EA theo thứ tự giảm dần
b) Tính chu vi hình ABCDE (tức là tính AB + BC + CD + DE + EA)
a, DE>AB>AE>CD>BC
b,chu vi hình ABCDE bằng 10, 4 cm
Đúng 0
Bình luận (0)
Vẽ hình để thấy được mỗi câu sau đây là saia) Hình gồm 3 đoạn thẳng được gọi là tam giácb) Hình gồm 3 đoạn thẳng đôi một cắt nhau được gọi là tam giác.c) Hình gồm 3 đoạn thẳng đôi một cắt nhau tạo ra 3 giao điểm (phân biệt) được gọi là tam giác.d) Hình gồm 3 đoạn thẳng AB, BC, CA được gọi là tam giác ABC.e) Hình gồm 3 điểm không thẳng hàng A, B, C được gọi là tam giác ABC.f) Một điểm không thuộc cạnh của tam giác ABC thì phải là đỉnh của tam giác đó.g) Một điểm không phải là đỉnh của tam giác AB...
Đọc tiếp
Vẽ hình để thấy được mỗi câu sau đây là sai
a) Hình gồm 3 đoạn thẳng được gọi là tam giác
b) Hình gồm 3 đoạn thẳng đôi một cắt nhau được gọi là tam giác.
c) Hình gồm 3 đoạn thẳng đôi một cắt nhau tạo ra 3 giao điểm (phân biệt) được gọi là tam giác.
d) Hình gồm 3 đoạn thẳng AB, BC, CA được gọi là tam giác ABC.
e) Hình gồm 3 điểm không thẳng hàng A, B, C được gọi là tam giác ABC.
f) Một điểm không thuộc cạnh của tam giác ABC thì phải là đỉnh của tam giác đó.
g) Một điểm không phải là đỉnh của tam giác ABC thì phải nằm trong tam giác đó.
h) Một điểm không nằm bên trong tam giác ABC thì phải nằm ngoài tam giác đó.
i) Hình gồm 2 góc được gọi là tam giác.
j) Hình gồm 3 góc mà các cạnh của nó đôi một cắt nhau tạo ra ba điểm được dọi là tam giác.
Cho tam giác ABC cân tại ,A kẻ một đường thẳng song song với BC cắt các cạnh AB và AC lần lượt tại D và .E
a) Tứ giác BDEC là hình gì? Tại sao?
b) Gọi O là giao điểm của BE và .CD Chứng minh AO là trung trực của .BC
a: Xét tứ giác BDEC có DE//BC
nên BDEC là hình thang
mà \(\widehat{DBC}=\widehat{ECB}\)
nên BDEC là hình thang cân
Đúng 1
Bình luận (0)
Cho tam giác ABC cân tại ,A kẻ một đường thẳng song song với BC cắt các cạnh AB và AC lần lượt tại D và .E
a) Tứ giác BDEC là hình gì? Tại sao?
b) Gọi O là giao điểm của BE và .CD Chứng minh AO là trung trực của .BC
cho ΔABC vuông tại A,tia phân giác của góc C cắt AB tại D, vẽ DE vuông góc với BC tại E
a) chứng minh rằng: ΔACD= ΔECD
b) tia ED cắt tia CA tại I. chứng minh tam giác DIB cân
c) gọi K là giao điểm của AE và CD, điểm M trên đoạn thẳng BK sao cho BM=2MK. EM cắt AB tại N. chứng minh N là trung điểm của AB.
a/ Xét tam giác ACD và ECD có:
ˆA=ˆD=90(gt)
ˆC1=ˆC2(gt)
CD chung
⇒ΔACD=ΔECD(c-g-c)
Đúng 1
Bình luận (0)
hình thang abcd có hai đáy là AB và CD Với AB = 5 CD phân giác của góc ABC cắt AD ở E và EA = 3 ED đoạn BE chia hình thang thành 2 đa giác tính tỉ số diện tích hai tam giác đó
Cho đường tròn tâm O , đường kính AB 2R . C là điểm chính giữa cung AB . Hai tiếp tuyến với đường tròn O tại A và C cắt nhau ở D.a) Chứng minh AOCD là hình vuôngb)Tính diện tích phần nằm ngoài hình thang ABCD của hình tròn O theo Rc) Trên đoạn DC lấy điểm E sao cho DE 1/3DC . Trên đoạn BC lấy điểm F sao cho cho EFEA . Kẻ FG vuông góc với đường thẳng DC ( G thuộc DC) . Tính dộ dài đoạn thẳng CG theo R .d) Chứng minh AECF là tứ giác nội tiếp
Đọc tiếp
Cho đường tròn tâm O , đường kính AB = 2R . C là điểm chính giữa cung AB . Hai tiếp tuyến với đường tròn O tại A và C cắt nhau ở D.
a) Chứng minh AOCD là hình vuông
b)Tính diện tích phần nằm ngoài hình thang ABCD của hình tròn O theo R
c) Trên đoạn DC lấy điểm E sao cho DE = 1/3DC . Trên đoạn BC lấy điểm F sao cho cho EF=EA . Kẻ FG vuông góc với đường thẳng DC ( G thuộc DC) . Tính dộ dài đoạn thẳng CG theo R .
d) Chứng minh AECF là tứ giác nội tiếp
Cho đường tròn tâm O , đường kính AB 2R . C là điểm chính giữa cung AB . Hai tiếp tuyến với đường tròn O tại A và C cắt nhau ở D.a) Chứng minh AOCD là hình vuôngb)Tính diện tích phần nằm ngoài hình thang ABCD của hình tròn O theo Rc) Trên đoạn Dc lấy điểm E sao cho DE 1/3DC . Trên đoạn BC lấy điểm F sao cho cho EFEA . Kẻ FG vuông góc với đường thẳng DC ( G thuộc DC) . Tính dộ dài đoạn thẳng CG theo R .d) Chứng minh AECF là tứ giác nội tiếp
Đọc tiếp
Cho đường tròn tâm O , đường kính AB = 2R . C là điểm chính giữa cung AB . Hai tiếp tuyến với đường tròn O tại A và C cắt nhau ở D.
a) Chứng minh AOCD là hình vuông
b)Tính diện tích phần nằm ngoài hình thang ABCD của hình tròn O theo R
c) Trên đoạn Dc lấy điểm E sao cho DE = 1/3DC . Trên đoạn BC lấy điểm F sao cho cho EF=EA . Kẻ FG vuông góc với đường thẳng DC ( G thuộc DC) . Tính dộ dài đoạn thẳng CG theo R .
d) Chứng minh AECF là tứ giác nội tiếp
Cho đường tròn tâm O , đường kính AB 2R . C là điểm chính giữa cung AB . Hai tiếp tuyến với đường tròn O tại A và C cắt nhau ở D.a) Chứng minh AOCD là hình vuôngb)Tính diện tích phần nằm ngoài hình thang ABCD của hình tròn O theo Rc) Trên đoạn Dc lấy điểm E sao cho DE 1/3DC . Trên đoạn BC lấy điểm F sao cho cho EFEA . Kẻ FG vuông góc với đường thẳng DC ( G thuộc DC) . Tính dộ dài đoạn thẳng CG theo R .d) Chứng minh AECF là tứ giác nội tiếp
Đọc tiếp
Cho đường tròn tâm O , đường kính AB = 2R . C là điểm chính giữa cung AB . Hai tiếp tuyến với đường tròn O tại A và C cắt nhau ở D.
a) Chứng minh AOCD là hình vuông
b)Tính diện tích phần nằm ngoài hình thang ABCD của hình tròn O theo R
c) Trên đoạn Dc lấy điểm E sao cho DE = 1/3DC . Trên đoạn BC lấy điểm F sao cho cho EF=EA . Kẻ FG vuông góc với đường thẳng DC ( G thuộc DC) . Tính dộ dài đoạn thẳng CG theo R .
d) Chứng minh AECF là tứ giác nội tiếp
