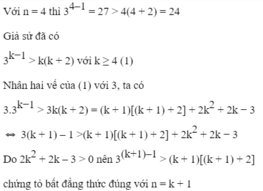Chứng minh phân thức 2 n - 1 4 n 2 - 2 là tối giản với mọi số tự nhiên n

Những câu hỏi liên quan
Chứng minh rằng n7+n2+1/n8+n+1 chưa phải là phân thức tối giản
Chứng minh các bất đẳng thức sau 3n − 1 > n(n + 2) với n ≥ 4
Chứng minh phân số 2.n+3/4.n+1 là phân số tối giản.
\(\frac{n+1}{2n+3}\) như này phải ko
Chứng minh phân thức 3 n + 1 5 n + 2 (với n ∈ N) là tối giản
Hướng dẫn giải:
Gọi ƯCLN của 2n + 1 và 5n + 3 là d
⇒ (3n + 1) ⋮ d và (5n + 2) ⋮ d
⇒ [3(5n + 2) - 5(3n + 1)] ⋮ d
⇒ 1 ⋮ d, với ∀n ∈ N
⇒ d = 1 hoặc d = -1
Vậy phân thức đã cho tối giản với ∀n ∈ N
Đúng 1
Bình luận (0)
Chứng minh rằng phân thức A = \(\dfrac{n+3}{n+2}\) tối giản
Tính giá trị của biểu thức A tại x = -2
ĐK:n≠-2
Gọi \(d=ƯCLN\left(n+3,n+2\right)\)
\(\Rightarrow n+3⋮d;n+2⋮d\\ \Rightarrow n+3-n-2⋮d\\ \Rightarrow1⋮d\\ \Rightarrow d=1\)
Vậy n+3 và n+2 nctn hay \(\dfrac{n+3}{n+2}\) tối giản
Với n=-2 trái vs ĐKXĐ nên A ko xác định
Đúng 2
Bình luận (0)
Chứng minh phân thức - n + 3 n - 4 (với n ∈ N) là tối giản:
Hướng dẫn giải:
Gọi ƯCLN của –n + 3 và n - 4 là d
⇒ (-n + 3)⋮ d và (n - 4)⋮ d
⇒ [(-n + 3) +(n - 4)] ⋮ d
⇒ -1⋮ d
⇒ d = 1 hoặc d = -1
Vậy phân thức đã cho là tối giản với ∀n ∈ N
Đúng 0
Bình luận (0)
Bài 1: Cho phân thức : P = (x+1/x-1 + 1-3x/x^3+x) : x-1/x^2+1. a)Tìm điều kiện của x để giá trị của phân thức được xác định.
b)Rút gọn P.Tính giá trị của P tại x = 6.
c) Tìm x để phân thức có giá trị là số nguyên.
Bài 2: Chứng minh đẳng thức : 1/n(n+1)=1/n - 1/n+1; Tính : a + a^2/1-a + 1/a+1.
1/Tìm x :
a/ |x+8| = 10
b/ (x+ 1/8) : 2/3 = 3- 3/4
2/
a/ Cho biểu thức A= 5/n-1 ; ( n thuộc Z )
Tìm điều kiện của n để A là phân số ? Tìm tất cả giá trị số nguyên cuả n để A là số nguyên ?
b/ CHỨNG MINH :
Phân số n/n+1 tối giản
( n thuộc N; n khác 0 )
c/ CHỨNG MINH :
1/1.2 + 1/2.3 + 1/3.4 + 1/4.5 +...+ 1/48.49 + 1/49.50 < 1
Chứng minh rằng:
\(\frac{n^2+n+1}{n^4+n^2+1}\)( n thuộc N*) không là phân số tối giản
Chứng minh phân thức \(\dfrac{3-n}{n-4}\) là tối giản:
Gọi d=ƯCLN(-n+3,n-4)
\(\Rightarrow-n+3⋮d;n-4⋮d\\ \Rightarrow-n+3+n-4⋮d\\ \Rightarrow-1⋮d\\ \Rightarrow d=1\\ \RightarrowƯCLN\left(-n+3,n-4\right)=1\)
Vậy ...
Đúng 2
Bình luận (0)