Hàm số y = x8 + (x4 – 1) 2 + 5 đạt giá trị lớn nhất, giá trị nhỏ nhất trên đoạn [0;2] lần lượt tại hai điểm có hoành độ x1; x2. Khi đó tích x1.x2 có giá trị bằng:
A. 1.
B. 2.
C. 3/2.
D. 0.
Biết rằng giá trị lớn nhất của hàm số y = | x 4 - 38 x 2 + 120 x + 4 m | trên đoạn [0;2] đạt giá trị nhỏ nhất. Khi đó giá trị của tham số m bằng
A. -12
B. -13
C. -14
D. -11
Chọn B
Xét f(x) = x 4 - 38 x 2 + 120 x + 4 m trên đoạn [0;2] ta có:
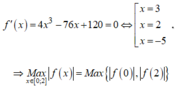
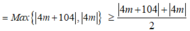
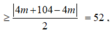
Dấu “=” xảy ra khi và chỉ khi ![]()
Nhận xét: Với trắc nghiệm thì ta thử đáp án được đáp án B
Tính giá trị lớn nhất và nhỏ nhất của hàm số:
y = x 4 - 3 x 2 + 2 trên các đoạn [0; 3] và [2; 5]
TXĐ: D = R
y ' = 4 x 3 - 6 x
y’ = 0 ⇔ 2x.(2x2 – 3) = 0 ⇔ 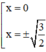
+ Xét hàm số trên [0 ; 3] :
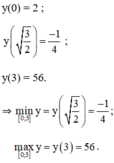
+ Xét hàm số trên [2; 5].
y(2) = 6;
y(5) = 552.
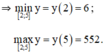
Gọi m và M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = x 4 - 2 x 3 + 3 trên đoạn [0; 2]. Tính giá trị của biểu thức M + 2m.
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Đáp án D
Ta có ![]() liên tục trên đoạn
liên tục trên đoạn ![]() .
.
Ta có ![]()
 .
.
![]() .
.
Vậy m=2 và M = 11, do đó ![]() .
.
Có bao nhiêu số nguyên m để giá trị nhỏ nhất của hàm số y = x 4 - 38 x 2 + 120 x + 4 m trên đoạn [0;2] đạt giá trị nhỏ nhất
A. 26
B. 13
C. 14
D. 27
Xét u = x 4 - 38 x 2 + 120 x + 4 m trên đoạn [0;2] ta có
![]()
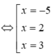
Vậy
Khi đó
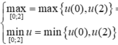
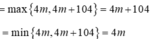
![]()
⇔ - 26 ≤ m ≤ 0
Có 27 số nguyên thoả mãn.
Chọn đáp án D.
Có bao nhiêu số nguyên m để giá trị nhỏ nhất của hàm số y = | x 4 - 38 x 2 + 120 x + 4 m | trên đoạn [0;2] đạt giá trị nhỏ nhất.
A. 26
B. 13
C. 14
D. 27
Chọn D
Xét ![]() trên đoạn [0;2], ta có:
trên đoạn [0;2], ta có:
Vậy 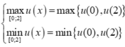
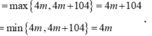
Cách 1:
Nếu 4m > 0 thì ![]()
Nếu 4m + 104 < 0
⇔
m < -126 thì ![]()
Nếu ![]() thì
thì ![]() Vậy có 27 số nguyên thỏa mãn.
Vậy có 27 số nguyên thỏa mãn.
Cách 2:
Khi đó ![]()
![]()
Có 27 số nguyên thoả mãn.
Có bao nhiêu số nguyên m để giá trị nhỏ nhất của hàm số y = x 4 - 38 x 2 + 120 x + 4 m trên đoạn 0 ; 2 đạt giá trị nhỏ nhất.
A. 26
B. 13
C. 14
D. 27
Chọn đáp án D.
Xét y = x 4 - 38 x 2 + 120 x + 4 m trên đoạn 0 ; 2 ta có
![]()
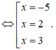
Vậy
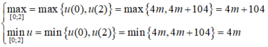
![]()
![]()
![]()
Có 27 số nguyên thoả mãn.
Cho hàm số y = x 4 - 4 x 3 + 4 x 2 + a . Gọi M; m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên đoạn [0; 2] . Có bao nhiêu số nguyên a thuộc đoạn [ -3; 3] sao cho M≤ 2m?
A. 4
B. 5
C. 6
D. 3
+ Xét hàm số y= x4- 4x3+ 4x2+ a trên đoạn [ 0; 2].
Ta có đạo hàm y’ = 4x3-12x2+ 8x,
y
'
=
0
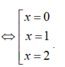
Khi đó; y( 0) = y( 2) = a; y( 1) = a+ 1
+ Nếu a≥ 0 thì M= a+ 1,m = a.
Để M ≤ 2m khi a≥ 1, suy ra a ∈ 1 ; 2 ; 3 thỏa mãn
+ Nếu a≤ - 1 thì M = a = - a , m = a + 1 = - a - 1 .
Để M≤ 2m thì a≤ -2, suy ra a a ∈ - 2 ; - 3
Vậy có 5 giá trị nguyên của a thỏa mãn yêu cầu.
Chọn B.
Tìm m để giá trị lớn nhất của hàm số y = x 2 + 2 x + m - 4 trên đoạn [-2; 1] đạt giá trị nhỏ nhất. Giá trị của m là
A. 4
B. 3
C. 1
D. 2
y = x 2 + 2 x + m - 4 = ( x + 1 ) 2 + m - 5
Ta có ( x + 1 ) 2 + m - 5 ∈ m - 5 ; m - 1
Giá trị lớn nhất của hàm số y = x 2 + 2 x + m - 4 trên đoạn[ -2; 1] đạt giá trị nhỏ nhất khi
m - 5 < 0 m - 1 > 0 5 - m = m - 1 ⇔ m = 3
Chọn B.
Cho các số thực x 1 , x 2 , x 3 , x 4 thỏa mãn 0 < x 1 < x 2 < x 3 < x 4 và hàm số y=f(x). Biết hàm số y=f’(x) có đồ thị như hình vẽ. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn 0 ; x 4 . Đáp áp nào sau đây đúng?
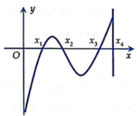
A. M + m = f 0 + f x 3 .
B. M + m = f x 3 + f x 4 .
C. M + m = f x 1 + f x 2 .
D. M + m = f 0 + f x 1 .