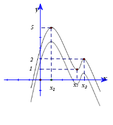
Cho hàm số y = f x , y = g x liên tục trên ℝ và có đồ thị các đạo hàm (đồ thị y = g ' x là đường đậm hơn) như hình vẽ
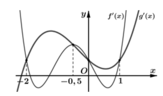
Hàm số h x = f x - 1 - g x - 1 nghịch biến trên khoảng nào dưới đây?
A. 1 2 ; 1
B. - 1 ; 1 2
C. 1 ; + ∞
D. 2 ; + ∞
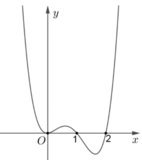
Cho hàm số y = f ( x ) có đạo hàm liên tục trên ℝ và có đồ thị hàm số y = f ' ( x ) như hình vẽ. Đặt g ( x ) = f ( x 3 ) . Tìm số điểm cực trị của hàm số y = g ( x )
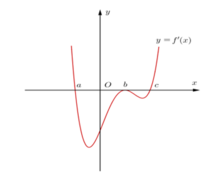
A. 3
B. 5
C. 4
D. 2
Cho hàm số y= f(x) xác định và liên tục trên R , có đồ thị của hàm số y= f’(x) như hình vẽ sau.
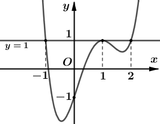
Đặt g(x) = f(x) + x. Tìm số cực trị của hàm số y= g(x) ?
A. 1.
B. 2.
C. 3.
D. 4.
Chọn B
Ta có g’(x) = f’(x) + 1.
Đồ thị của hàm số y= g’(x) là phép tịnh tiến đồ thị của hàm số y= f’(x) theo phương song song với Oy lên trên 1 đơn vị.
Khi đó đồ thị hàm số y= g’(x) cắt trục hoành tại hai điểm phân biệt.
=> Hàm số y= g(x) có 2 điểm cực trị.
Cho hàm số y= f( x) ) liên tục trên R. Hàm số y= f’ (x) có đồ thị như hình vẽ. Hàm số y = g ( x ) = f ( x ) + 2017 - 2018 x 2017 có bao nhiêu cực trị?
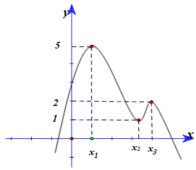
A. 1.
B. 2.
C. 3.
D. 4.
Ta có ![]()
Suy ra đồ thị của hàm số g’ (x) là phép tịnh tiến đồ thị hàm số y= f’ (x) theo phương Oy xuống dưới ![]() đơn vị.
đơn vị.
Ta có ![]() và dựa vào đồ thị của hàm số y= f’ (x), ta suy ra đồ thị của hàm số g’ (x) cắt trục hoành tại 4 điểm.
và dựa vào đồ thị của hàm số y= f’ (x), ta suy ra đồ thị của hàm số g’ (x) cắt trục hoành tại 4 điểm.
Chọn D.
Cho hàm số y = f(x) có đạo hàm liên tục trên R và có đồ thị của hàm số y = f’(x) như hình vẽ. Đặt g ( x ) = 3 f ( x ) + x 3 - 3 x 2 . Tìm số điểm cực trị của hàm số y = g(x)
A. 1.
B. 2.
C. 3.
D. 0.
Đáp án B
Ta có
![]() .
.
![]() .
.
Hình bên dưới là đồ thị của hàm số ![]() và
và ![]() .
.
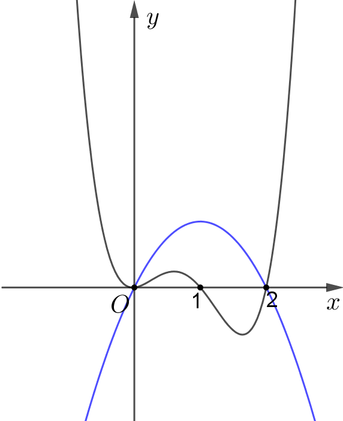
Dựa vào hình vẽ ta thấy đồ thị hàm số ![]() và
và ![]() cắt nhau tại 2 điểm phân biệt, đồng thời
cắt nhau tại 2 điểm phân biệt, đồng thời ![]() khi
khi ![]() hoặc
hoặc ![]() ,
, ![]() khi
khi ![]() .
.
Do đó ![]() đổi dấu qua
đổi dấu qua ![]() ,
, ![]() .
.
Vậy hàm số g(x) có hai điểm cực trị.
Cho hàm số y = f ( x ) liên tục trên R và có đồ thị hàm số y = f ' ( x ) như hình bên:
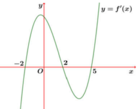
Hỏi hàm số g ( x ) = f ( 3 - 2 x ) nghịch biến trên khoảng nào sau đây?
A. (-1;+∞)
B. (-∞;-1)
C. (1;3)
D. (0;2)
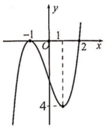
Cho hàm số y=f(x) có đạo hàm trên R. Đường cong hình vẽ bên là đồ thị hàm số y=f '(x) (Hàm số y=f '(x) liên tục trên R. Xét hàm số g ( x ) = f ( x 2 - 2 ) . Mệnh đề nào dưới đây là sai?
A. Hàm số y=g(x) đồng biến trên khoảng (-2;-1)
B. Hàm số y=g(x) đồng biến trên khoảng 2 ; + ∞
C. Hàm số y=g(x) nghịch biến trên khoảng (-1;0)
D. Hàm số y=g(x) nghịch biến trên khoảng (0;2)
Cho hàm số y = f(x) có đạo hàm trên R. Đường cong trong hình vẽ bên là đồ thị của hàm số y = f’(x), (y = f’(x) liên tục trên R). Xét hàm số g(x) = f(x2 - 2). Mệnh đề nào dưới đây sai?

A. Hàm số g(x) nghịch biến trên (-∞;-3)
B. Hàm số g(x) có 3 điểm cực trị
C. Hàm số g(x) nghịch biến trên (-1;0)
D. Điểm cực đại của hàm số là 0
Cho hàm số y = f(x) có đạo hàm liên tục trên ℝ . Đồ thị hàm số y = f'(x) được cho như hình vẽ bên.
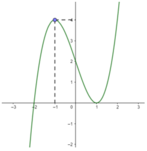
Số điểm cực trị của hàm số g(x) = f(x-2017) - 2018x + 2019 là:
A. 1.
B. 3.
C. 2.
D. 0.
Chọn A
Ta có: g(x) = f(x-2017) - 2018x + 2019.
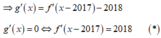
Nhận xét: tịnh tiến đồ thị hàm số y = f'(x) sang bên phải theo phương của trục hoành 2017 đơn vị ta được đồ thị hàm số y = f'(x-2017) . Do đó, số nghiệm của phương trình f'(x) = 2018 bằng số nghiệm của phương trình (*).
Dựa vào đồ thị ta thấy phương trình (*) có nghiệm đơn duy nhất hay hàm số đã cho có duy nhất 1 điểm cực trị.
Cho hàm số y = f(x) có đạo hàm liên tục trên i. Đồ thị hàm số y = f’(x) như hình bên dưới
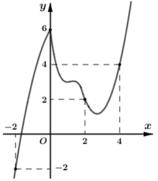
Hàm số g(x) = 2 f(x) - x 2 đồng biến trên khoảng nào trong các khoảng sau đây?
![]()
![]()
![]()
![]()
Cho hàm số y= f( x) có đạo hàm liên tục trên R. Đồ thị hàm số y= f’(x) như hình bên dưới
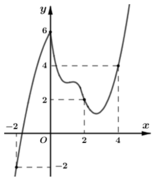
Hàm số g(x) = 2 . f(x) – x2 đồng biến trên khoảng nào trong các khoảng sau đây?
A. ( - ∞ ; - 2 )
B. (-2; 2)
C. (2; 4)
D. ( 2 ; + ∞ )