Cho hàm số y=f(x) có đạo hàm trên R và có đồ thị như hình vẽ
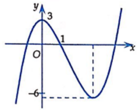
Đặt g x = 2 f x − 3 f x . Tìm số nghiệm của phương trình g’(x)=0
A. 5
B. 3
C. 2
D. 6
Cho hàm số f(x) có đạo hàm trên R và có đồ thị hàm y = f'(x) như hình vẽ. Xét hàm số g ( x ) = f ( x 2 - 2 ) . Mệnh đề nào dưới đây sai?
A . H à m s ố g ( x ) đ ồ n g b i ế n t r ê n ( 2 ; + ∞ ) .
B . H à m s ố g ( x ) n g h ị c h b i ế n t r ê n ( - 1 ; 0 ) .
C . H à m s ố g ( x ) n g h ị c h b i ế n t r ê n ( 0 ; 2 ) .
D . H à m s ố g ( x ) n g h ị c h b i ế n t r ê n ( - ∞ ; - 2 ) .
Cho hàm số y=f(x) có đạo hàm trên R và có đồ thị y=f’(x) như hình vẽ. Xét hàm số g ( x ) = f ( x 2 - 2 )
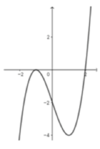
Mệnh đề nào sau đây sai?
A. Hàm số g(x) nghịch biến trên (0;2)
B. Hàm số g(x) đồng biến trên (2;+∞)
C. Hàm số g(x) nghịch biến trên (-∞;-2)
D. Hàm số g(x) nghịch biến trên (-1;0)
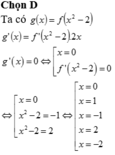
g’(x) đổi dấu qua các nghiệm đơn hoặc bội lẻ, không đổi dấu qua các nghiệm bội chẵn nên ta có bảng xét dấu g’(x)

Cho hàm số y = f(x) có đạo hàm trên R và có đồ thị y = f'(x) như hình vẽ.
Xét hàm số g(x) = f( x 2 -2).
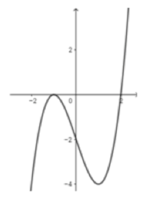
Mệnh đề nào sau đây sai?
A. Hàm số g(x) nghịch biến trên (0;2).
B. Hàm số g(x) đồng biến trên (2;+ ∞ ).
C. Hàm số g(x) nghịch biến trên (- ∞ ;-2).
D. Hàm số g(x) nghịch biến trên (-1;0).
Chọn D
Ta có g(x) = f( x 2 -2).
![]()
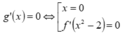
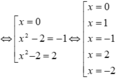
Ta có g'(3) = 6.f'(7) > 0, g’(x) đổi dấu qua các nghiệm đơn hoặc bội lẻ, không đổi dấu qua các nghiệm bội chẵn nên ta có bảng xét dấu g’(x):
![]()
Suy ra đáp án là D.
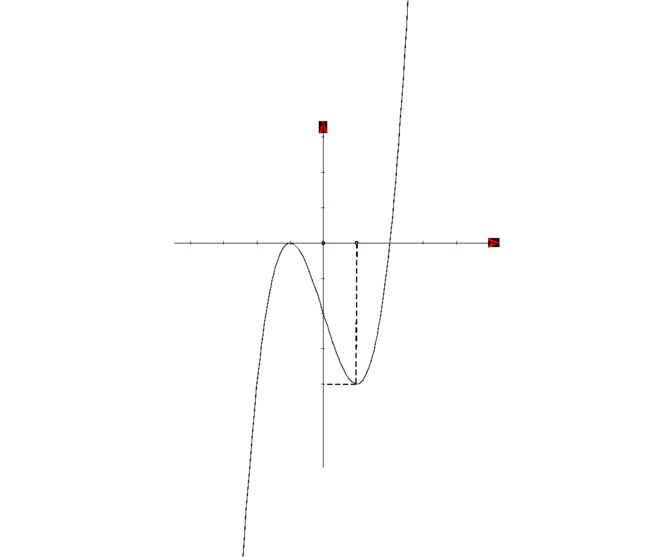
Cho hàm số y=f(x) có đạo hàm liên tục trên R và có đồ thị hàm y=f '(x) như hình vẽ. xét hàm số g(x)=f(2-x^2). Mệnh đề nào dưới đây sai?
A. Hàm số ![]() đạt cực trị tại
đạt cực trị tại ![]() .
.
B. Hàm số ![]() nghịch biến trên
nghịch biến trên ![]() .
.
C. Hàm số ![]() đồng biến trên
đồng biến trên ![]() .
.
D. Hàm số ![]() đồng biến trên
đồng biến trên ![]() .
.
Cho hàm số y = f(x) có đạo hàm trên R và có đồ thị của hàm số y = f'(x) như hình vẽ. Xét hàm số g(x) = f x 2 - 2
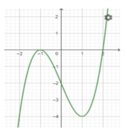
Mệnh đề nào sau đây sai?
A. Hàm số g(x) nghịch biến trên (0;2)
B. Hàm số g(x) đồng biến trên (2;+ ∞ )
C. Hàm số g(x) nghịch biến trên (- ∞ ;-2)
D. Hàm số g(x) nghịch biến trên (-1;0).
Chọn D.
Xét g(x) = f x 2 - 2
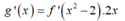
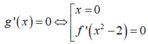
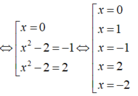
Bảng xét dấu g’(x):

Suy ra hàm số g(x) nghịch biến trên (-1;0) là sai.
Cho hàm số y=f(x) có đạo hàm trên R. Đồ thị hàm số y=f '(x) như hình vẽ bên dưới. Hỏi đồ thị hàm số g(x)=f(x)-x có bao nhiêu điểm cực trị?
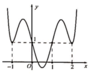
A. 1
B. 2
C. 3
D. 4
Cho hàm số y=f(x) có đạo hàm trên R. Đồ thị hàm số y=f’(x) như hình vẽ bên dưới. Hỏi đồ thị hàm số g(x)=-x-f(x) đạt cực đại tại?
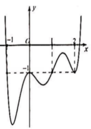
A. x = -1
B. x = 0
C. x = 1
D. x = 2
Cho hàm số y = f(x) có đạo hàm liên tục trên R đồ thị hàm số y = f’(x) như hình vẽ.
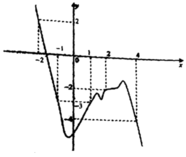
Biết f(2) = –6, f(–4) = –10 và hàm số g(x) = f(x)+ x 2 2 , g(x) có ba điểm cực trị.
Phương trình g(x) = 0?
A. Có đúng 2 nghiệm
B. Vô nghiệm
C. Có đúng 3 nghiệm
D. Có đúng 4 nghiệm
Đáp án B
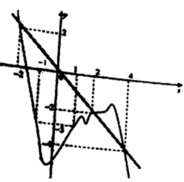
Phương pháp: Lập bảng biến thiên của g(x) và đánh giá số giao điểm của đồ thị hàm số y = g(x) và trục hoành.
Cách giải: 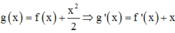
![]()
Xét giao điểm của đồ thị hàm sốy = f’(x) và đường thẳng y = -x ta thấy, hai đồ thị cắt nhau tại ba điểm có hoành độ là: -2;2;4 tương ứng với 3 điểm cực trị của y = g(x).
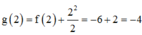
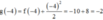
Bảng biến thiên:
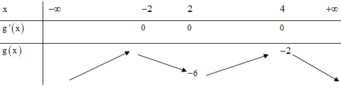
Dựa vào bảng biến thiên ta thấy ![]() => phương trình g(x) = 0 không có nghiệm
=> phương trình g(x) = 0 không có nghiệm ![]()
Cho hàm số y = f(x) có đạo hàm trên R và có đồ thị hàm số y = f'(x) như hình vẽ.
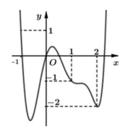
Hàm số g ( x ) = 2 f ( x ) + x 2 đạt cực đại tại điểm?
A. x = -1
B. x = 0
C. x = 1
D. x = 2


Có bảng dấu
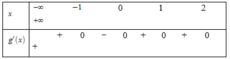
Từ đó suy ra hàm số g(x) đạt cực đại tại điểm x = -1
Cho đồ thị hàm số y = f(x) có đạo hàm trên R thỏa mãn f(2) = f(-2) = 0 và đồ thị hàm số y = f'(x) có dạng như hình vẽ. Hàm số y = f ( x ) 2 nghịch biến trên khoảng nào trong các khoảng sau?
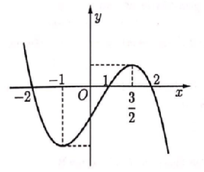
A. - 1 ; 3 2
B. (-2;-1)
C. (-1;1)
D. (1;2)