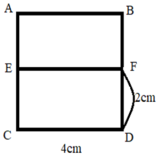
Cho hình vẽ, chọn câu trả lời đúng nhất. Biết EFCD, AEFB là hình chữ nhật. E,F lần lượt là trung điểm của AC, BD. Hỏi ABCD là hình gì?
A. Hình thoi
B. Hình lục giác
C. Hình bình hành
D. Hình vuông
Bài 1. Cho tứ giác ABCD có E, F, G, H lần lượt là trung điểm của AB, BC, CD, DA. Biết AC = BD và AC vuông góc BD. Chứng minh: a) EFGH là hình bình hành. b) EFGH là hình chữ nhật. c) EFGH là hình thoi. d) EFGH là hình vuông
Cho hình bình hành ABCD. E, F lần lượt là trung điểm của AB, CD. Đường thẳng BD cắt AF và CE lần lượt tại G, H.
a) tứ giác EFGH là hình gì?
b) hình bình hành ABCD có thêm điều kiện gì thì EFGH là hình chữ nhật, hình thoi
Ko có cái quần què gì để gửi nên viết ra đây các OLMERS đừng trả lời nhé plz
ko trả lời ra dưới câu hỏi mình nhé các OLMERS. Ai trả lời dưới câu hỏi là coi như không biết đọc chữ đáy nhé :))
Bài 1: Cho tứ giác ABCD có BC=AD và BC không song song với AD. Gọi M,N,P,Q,E,F lần lượt là trung điểm của các đoạn thẳng AB,BC,CA,DA,AC,BD.
a) Chứng minh tứ giác MEPF là hình thoi
b) Chứng minh các đoạn thẳng MP,NQ,EF cùng cắt nhau tại một điểm
c) Tìm thêm điều kiện của tứ giác ABCD để N,E,F,Q thẳng hàng
Bài 2: Cho tam giác ABC vuông tại A ( AB<AC ),M là trung điểm của BC,từ M kẻ đường thẳng song song với AC,AB lần lượt cắt AB tại E, cắt AC tại F.
a) Chứng minh EFCB là hình thang
b) Chứng minh AEMF là hình chữ nhật
c) Gọi O là trung điểm của AM.Chứng minh E và F đối xứng qua O
d) Gọi D là trung điểm của MC. Chứng minh OMDF là hình thoi.
Bài 3:Cho hình bình hành ABCD , trên AC lấy 2 điểm M và N sao cho AM=CN
a) Tứ giác BNDM là hình gì?
b) hình bình hành ABCD phải thêm điều kiện gì? Thì BNDM là hình thoi
c) BM cắt AD tại K . Xác định vị trí của M để K là trung điểm của AD.
d) Hình bình hành ABCD thỏa mãn cả 2 điều kiện ở b,c thì phải thêm điều kiện gì để BNDM là hình vuông
Cho hình bình hành ABCD. Gọi E. F lần lượt là trung điểm của AB và CD, G và H lần lượt là giao điểm của BD với AF và CE.
a, C/minh: Tứ giác AECF, GEHF là hình bình hành
b, C/minh: DG = GH = HB
c, Để tứ giác GEHF là hình chữ nhật thì hình bình hành ABCD cần thêm điều kiện gì ?
d, Để tứ giác GEHF là hình thoi thì hình bình hành ABCD cần thêm điều kiện gì ?
Cho hình bình hành ABCD. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA
a) Chứng minh tứ giác MNPQ là hình bình hành
b) Hình bình hành ABCD cần thêm điều kiện gì để MNPQ là hình chữ nhật, hình thoi, hình vuông?
c) Gọi O là giao điểm của AC,BD.Chứng minh: M,O,P thẳng hàng
d) Chứng minh : AC, BD, QN đồng qui
a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của BC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//AC và MN=AC/2(1)
Xét ΔADC có
Q là trung điểm của AD
P là trung điểm của CD
Do đó: QP là đường trung bình của ΔADC
Suy ra: QP//AC và QP=AC/2(2)
Từ (1) và (2) suy ra MN//PQ và MN=PQ
hay MNPQ là hình bình hành
cho hình bình hành ABCD. gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, DA.
a/ CM tứ giác EFGH là hình bình hành.
b/ Khi hình bình hành ABCD là hình chữ nhật, hình thoi thì EFGH là hình gì? Chứng minh.
Xét \(\Delta ADB\):
\(AE=EB\left(gt\right)\)
\(HD=HA\left(gt\right)\)
\(\Rightarrow HE\)là đường trung binh cũa \(\Delta ADB\).
\(\Rightarrow HE\)//\(DB\)và \(HE=\frac{1}{2}DB\left(1\right)\)
Xét \(\Delta CDB:\)
\(FB=FC\left(gt\right)\)
\(GC=GD\left(gt\right)\)
\(\Rightarrow GF\) là dường trung bình của \(\Delta CBD\).
\(\Rightarrow GF\)//\(DB\)và \(GF=\frac{1}{2}DB\left(2\right)\)
Từ \(\left(1\right)\left(2\right)\Rightarrow\)\(HE\)//\(GF\)và \(HE=GF\)
Vậy tứ giác \(EFGH\)là hình bình hành.
b) Xét \(\Delta AEH\)và \(\Delta EBF\):
\(AE=EB\left(gt\right)\)
Góc A = Góc B = 90o (ABCD là hình chữ nhật)
\(AD=BC\Rightarrow\frac{1}{2}AD=\frac{1}{2}BC\Rightarrow AH=BF\)
\(\Rightarrow\Delta AEH=\Delta EBF\left(c.g.c\right)\)
\(\Rightarrow HE=HF\)
mà tứ giác EFGH là hình bình hành.
Vậy hình bình hành \(EFGH\)là hình thoi.
Ta cm theo qui tắc đường trung bình của tam giác là ra ngay
Ta có E là trung điểm của AB,F là trung điểm của BC>>>EF=1/2AC.tuơng tự HG=1/2 AC>>>EF=HG
CM ttự với cặp còn lại là ra thôi
Bài 1. Cho tứ giác ABCD. Gọi E, F, G, H lần lượt là trung điểm của AB, BC, CD, DA. Các đường chéo AC, BD của tứ giác ABCD thoả điều kiện gì thì tứ giác EFGH là:
a) Hình chữ nhật.
b) Hình thoi.
c) Hình vuông.
Bài 2. Cho tam giác ABC cân tại A, trung tuyến AM. Gọi I là trung điểm của AC, K là điểm đối xứng của điểm M qua điểm I.
a) Tứ giác AMCK là hình gì?
b) Tứ giác AKMB là hình gì?
c) Có trường hợp nào của tam giác ABC để tứ giác AKMB là hình thoi.
ĐS: a) AMCK là hình chữ nhật b) AKMB là hình bình hành c) Không.
cho hình bình hành ABCD có AB=2AD. Gọi E,F lần lượt là trung điểm của AB và CD. Gọi M là giao điểm của AF và DE. Gọi N là giao điểm của BF và CE.
a) C/m tứ giác AEFD là hình thoi
b) Tứ giác AECF là hình gì? Tại sao?
c) C/m tứ giác EMFN là hình chữ nhật
d) Hình bình hành ABCD có thêm điều kiện gì thì tứ giác EMFN là hình vuông?