Đơn vị của nhiệt dung riêng của vật là:
A. J/kg
B. kg/J
C. J/kg.K
D. kg/J.K
Xác định lượng nhiệt cần cung cấp cho cục nước đá khối lượng 0,2 kg ở -20 ° C biến hoàn toàn thành hơi nước ở 100 ° C. Cho biết nước đá có nhiệt nóng chảy riêng là 3,4. 10 5 J/kg và nhiệt dung riêng là 2,09. 10 3 J/kg.K ; nước có nhiệt dung riêng là 4,18. 10 3 J/kg.K và nhiệt hoá hơi riêng là 2,3. 10 3 J/kg.
Nhiệt lượng cần phải cung cấp để làm cho một cục nước đá có khối lượng 200 g nước đá ở -20 ° C tan thành nước và được đun sôi để biến hoàn toàn thành hơi nước ở 100 ° C
Q = c đ m( t 1 - t 0 ) + λ m + c n m( t 2 - t 1 ) + Lm
hay Q = m [ c đ ( t 1 - t 0 ) + λ + c n ( t 2 - t 1 ) + L]
Thay số, ta tìm được :
Q = 0,2. [2,09. 10 3 (0 - (-20)) + 3,4. 10 5 + 4,18. 10 3 (100 - 0) + 2,3. 10 6 ]
hay Q = 205 960 J ≈ 206 kJ
Xác định lượng nhiệt cần cung cấp để biến đổi 6,0 kg nước đá ở - 20 ° C thành hơi nước ở 100 ° C. Cho biết nước đá có nhiệt dung riêng là 2090 J/kg.K và nhiệt nóng chảy riêng là 3,4. 10 5 J/kg, nước có nhiệt dung riêng là 4180 J/kg.K và nhiệt hóa hơi riêng là 2,3. 10 6 J/kg. Bỏ qua sự mất mát nhiệt do bình chứa hấp thụ và do truyền ra bên ngoài.
Lượng nhiệt cần cung cấp để biến đổi m = 6,0 kg nước đá ở nhiệt độ t 1 = -20 ° C biến thành hơi nước ở t 2 = 100 ° C có giá trị bằng :
Q = Q 1 + Q 2 + Q 3 + Q 4
trong đó lượng nhiệt Q 1 = c 1 m( t 0 - t 1 ) cung cấp cho m (kg) nước đá có nhiệt dung riêng c đ để nhiệt độ của nó tăng từ t 1 = -20 ° C đến t 0 = 0 ° C ; lượng nhiệt Q 0 = λ m cung cấp cho m (kg) nước đá có nhiệt nóng chảy riêng λ ở t 0 = 0 ° C tan thành nước ở cùng nhiệt độ ; lượng nhiệt Q 2 = c 0 m( t 2 - t 0 )
cung cấp cho m (kg) nước có nhiệt dung riêng c n để nhiệt độ của nó tăng từ t 0 = 0 ° C đến t 2 = 100 ° C ; lượng nhiệt Q 3 = Lm cung cấp cho m (kg) nước có nhiệt hoá hơi riêng L ở t 2 = 100 ° C biến thành hơi nước ở cùng nhiệt độ. Như vậy, ta có thể viết:
Q = c đ m( t 0 - t 1 ) + λ m + c n m( t 2 - t 0 ) + Lm
hay Q = m[ c đ ( t 0 - t 1 ) + λ + c n ( t 2 - t 0 ) + L]
Thay số, ta tìm được :
Q = 6,0. [2090.(0 + 20) + 3,4. 10 5 + 4180.(100 - 0) + 2,3. 10 6 ]
Q ≈ 186. 10 6 J.
Một bình nhôm khối lượng 0,5 kg chứa 4 kg nước ở nhiệt độ 20 oC. Người ta thả vào bình một miếng sắt có khối lượng 0,2 kg đã được nung nóng tới 500 oC. Cho nhiệt dung riêng của nhôm là 896 J/kg.K; của nước là 4,18.103 J/kg.K; của sắt là 0,46.103 J/kg.K. Nhiệt độ của nước khi bắt đầu có sự cân bằng nhiệt là:
A. 42,9 oC
B. 22,6 oC
C. 32,9 oC
D. 39,9 oC
Đáp án: C
Phương trình cân bằng nhiệt:
(mbcb + mnccnc).(tcb – t1) = msắtcsắt(t2 – tcb)
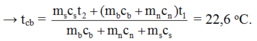
Một bình nhiệt lượng kế bằng thép khối lượng 0,1 kg chứa 0,5 kg nước ở nhiệt độ 15 ° C. Người ta thả một miếng chì và một miếng nhôm có tổng khối lượng 0,15 kg và nhiệt độ 100 ° C vào nhiệt lượng kế. Kết quả là nhiệt độ của nước trong nhiệt lượng kế tăng lên đến 17 ° C. Xác định khối lượng của miếng chì và miếng nhôm.
Cho biết nhiệt dung riêng của chì là 127,7 J/(kg.K), của nhôm là 836 J/(kg.K), của sắt là 460 J/(kg.K), của nước là 1 280 J/(kg.K). Bỏ qua sự mất mát nhiệt ra bên ngoài.
Độ lớn của nhiệt lượng toả ra và nhiệt lượng thu vào :
Q t o ả = c 1 m 1 t 2 - t + c 2 m 2 t 2 - t = c 1 m 1 t 2 - t + c 2 M - m 1 t 2 - t (1)
Q t h u = c m t - t 1 + c 0 m 0 t - t (2)
Từ (1) và (2) dễ dàng tính được :
m 1 = 0,104 kg = 104 g ; m 2 = 0,046 kg = 46 g.
Người ta thả một cục nước đá khối lượng 80 g ở 0 ° C vào một cốc nhôm đựng 0,4 kg nước ở 20 ° C đặt trong nhiệt lượng kế. Khối lượng cốc nhôm là 0,2 kg. Xác định nhiệt độ của nước trong cốc nhôm khi cục nước đá vừa tan hết. Cho biết nhiệt nóng chảy riêng của nước đá là 3,4. 10 5 J/kg , nhiệt dung riêng của nhôm là 880 J/kg.K và của nước là 4180 J/kg.K. Bỏ qua sự mất mát nhiệt do truyền ra ngoài.
Gọi λ là nhiệt nóng chảy riêng của cục nước đá khối lượng m 0 ở t 0 = 0 ° C ; còn c 1 , m 1 , c 2 , m 2 là nhiệt dung riêng và khối lượng của cốc nhôm và của lượng nước đựng trong cốc ở nhiệt độ t 1 = 20 ° C. Nếu gọi t ° C là nhiệt độ của nước trong cốc nhôm khi cục nước đá vừa tan hết thì lượng nhiệt do cục nước đá ở t 0 = 0 ° C đã thu vào để tan thành nước ở t ° C bằng :
Q = λ m 0 + c 2 m 0 (t - t 0 ) = m 0 ( λ + c 2 t)
Còn nhiệt lượng do cốc nhôm và lượng nước đựng trong cốc ở t 1 = 20 ° C. toả ra để nhiệt độ của chúng giảm tới toC (với t < t 1 ) có giá trị bằng :
Q'= ( c 1 m 1 + c 2 m 2 )( t 1 - t)
Theo định luật bảo toàn năng lượng, ta có :
Q' = Q ⇒ ( c 1 m 1 + c 2 m 2 ) ( t 1 - t) = m 0 ( λ + c 2 t)
Từ đó suy ra :
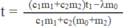
Thay số : t ≈ 3,7 ° C.
Một thỏi nhôm khối lượng 8,0 kg ở 20 ° C. Xác định lượng nhiệt cung cấp làm nóng chảy hoàn toàn thỏi nhôm này. Cho biết nhôm nóng chảy ở 658 ° C, có nhiệt nóng chảy riêng là 3,9. 10 5 J/kg và nhiệt dung riêng là 880 J/kg.K.
A. 5900kJ. B. 7612 kJ. C. 4700kJ. D. 470
Chọn đáp án B
Lượng nhiệt Q cung cấp để làm nóng chảy hoàn toàn thỏi nhôm khối lượng m = 8kg ở t 0 = 20°C có giá trị bằng:
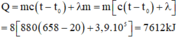
Câu 2: (3 điểm) Một miếng thép khối lượng m = 1,1 kg được nung đến 5000C rồi thả vào một ấm đựng 2 kg nước ở 200C, ấm làm bằng nhôm có khối lượng 0,5 kg. Cho nhiệt dung riêng của nước 4200 J/kg.K, nhôm là 880 J/kg.K, thép là 460 J/kg.K.
a. Tính nhiệt độ cuối cùng của hệ nếu bỏ qua sự mất mát nhiệt ra môi trường.
b. Nếu chỉ có 80% nhiệt lượng miếng thép tỏa ra truyền cho ấm nước thì nhiệt độ cân bằng của hệ là bao nhiêu.
Câu 2: (3 điểm) Một miếng thép khối lượng m = 1,1 kg được nung đến 5000C rồi thả vào một ấm đựng 2 kg nước ở 200C, ấm làm bằng nhôm có khối lượng 0,5 kg. Cho nhiệt dung riêng của nước 4200 J/kg.K, nhôm là 880 J/kg.K, thép là 460 J/kg.K.
a. Tính nhiệt độ cuối cùng của hệ nếu bỏ qua sự mất mát nhiệt ra môi trường.
b. Nếu chỉ có 80% nhiệt lượng miếng thép tỏa ra truyền cho ấm nước thì nhiệt độ cân bằng của hệ là bao nhiêu.
a)Gọi nhiệt độ cân bằng cuối cùng của hệ là \(t^oC\)
Nhiệt lượng miếng thép tỏa ra:
\(Q_{tỏa}=m_{thép}\cdot c_{thép}\cdot\left(t_1-t\right)\)
\(=1,1\cdot460\cdot\left(500-t\right)=506\cdot\left(500-t\right)\left(J\right)\)
Nhiệt lượng ấm nhôm thu vào:
\(Q_{thu}=\left(m_{ấm}\cdot c_{nhôm}+m_{nước}\cdot c_{nước}\right)\cdot\left(t_2-t\right)\)
\(=\left(0,5\cdot880+2\cdot4200\right)\left(t-20\right)=8840\left(t-20\right)\left(J\right)\)
Cân bằng nhiệt: \(Q_{tỏa}=Q_{thu}\)
\(\Rightarrow506\left(500-t\right)=8840\left(t-20\right)\)
\(\Rightarrow t\approx46^oC\)
b)Nếu chỉ có 80% nhiệt lượng thép tỏa ra thì:
\(Q_{tỏa}'=80\%Q_{tỏa}=506\cdot\left(500-t'\right)\cdot80\%=404,8\left(500-t'\right)\left(J\right)\)
Cân bằng nhiệt lúc này: \(Q_{tỏa}'=Q_{thu}\)
\(\Rightarrow404,8\left(500-t'\right)=8840\left(t'-20\right)\)
\(\Rightarrow t'\approx41^oC\)
một bình nhôm khối lượng 0,5 kg chứa 0,118 kg nước ở nhiệt độ 20oC . Người ta thả vào bình một miếng sắt khối lượng 0,2 kg đã được nung nóng tới 75oC . Xác định nhiệt độ của nước khi bắt đầu có sự cân bằng nhiệt . Bỏ qua sự truyền nhiệt ra môi trường bên ngoài . Nhiệt dung riêng của nhôm là 896 J/(kg.K) , của nước là 4,18.103 J/(kg.K) , của sắt là 0,46.103 J/(kg.K) .
Nhiệt lượng bình nhôm và nước thu vào là
\(Q_{thu} = Q_{Al}+Q_{nc} = c_{Al}m_{Al}(t-20)+c_{nc}m_{nc}(t-20) \) (1)
Nhiệt lượng miếng sắt tỏa ra khi thả vào bình nhôm chứa nước là
\(Q_{toa} = Q_{Fe} = c_{Fe}m_{Fe}(75-t) .(2)\)
Bỏ qua sự truyền nhiệt nên ta có khi có sự cân bằng nhiệt thì nhiệt lượng tỏa ra đúng bằng nhiệt lượng thu vào
\(Q_{thu} = Q_{toa}\)
=> \( c_{Al}m_{Al}(t-20)+c_{nc}m_{nc}(t-20) = c_{Fe}m_{Fe}(75-t) \)
Thay số thu được t = 24,890C.
Một bình nhôm khối lượng 0,5 kg chứa 0,118 kg nước ở nhiệt độ 20 oC. Người ta thả vào bình một miếng sắt khối lượng 0,2 kg đã được nung nóng tới 75 oC. Bỏ qua sự truyền nhiệt ra môi trường bên ngoài. Nhiệt dung riêng của nhôm là 0,92.103 J/(kg.K); của nước là 4,18.103 J(kg.K); của sắt là 0,46. 103 J(kg.K). Xác định nhiệt độ của nước khi bắt đầu có sự cân bằng nhiệt.
A. 29,8 oC
B. 26,8 oC
C. 25,8 oC
D. 24,8 oC
Đáp án: D
Nhiệt lượng mà nước thu vào cho đến khi cân bằng nhiệt:
Q1= m1c1Δt1
Nhiệt lượng mà bình nhôm thu vào cho đến khi cân bằng nhiệt:
Q2 = m2c2Δt2
Nhiệt lượng miếng sắt tỏa ra cho đến khi cân bằng nhiệt:
Q3= m3 c3 Δt3
Tổng nhiệt lượng thu vào bằng nhiệt lượng tỏa ra:
Q1 + Q2 = Q3
→ (m1c1 + m2c2)Δt1 = m3c3Δt3
Thay số ta được:
(0,118.4,18.103 + 0,5.0,92.103)(t - 20)
= 0,2.0,46.103(75 - t)
=> t = 24,8oC.
Vậy nhiệt độ cân bằng trong bình là:
![]()