Không dùng công thức nghiệm, tính tổng các nghiệm của phương trình 6 x 2 – 7 x = 0
A. − 7 6
B. 7 6
C. 6 7
D. - 6 7
Không dùng công thức nghiệm, tính tổng các nghiệm của phương trình 6 x 2 - 7x = 0
A. - 7 6
B. 7 6
C. 6 7
D. - 6 7
Không dùng công thức nghiệm, tính tổng các nghiệm của phương trình 6 x 2 - 7 x = 0
A. - 7 6
B. 7 6
C. 6 7
D. - 6 7
Không giải phương trình, dùng hệ thức Vi-ét, hãy tính tổng và tích các nghiệm của mỗi phương trình 5 x 2 + x + 2 = 0
Ta có: ∆ = 1 2 -4.5.2 = 1 - 40 = -39 < 0
Không giải phương trình, dùng hệ thức Vi-ét, hãy tính tổng và tích các nghiệm của mỗi phương trình 2 x 2 + 9x + 7 = 0
2 x 2 + 9x + 7 = 0
∆ = 9 2 - 4.2.7 = 81 - 56 = 25 > 0
Do đó, phương trình có hai nghiệm phân biệt
Theo hệ thức Vi – et ta có:
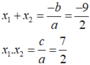
a) Cho phương trình $x^{2}-m x-10 m+2=0$ có một nghiệm $x_{1}=-4$. Tìm $m$ và nghiệm còn lại.
b) Cho phương trình $x^{2}-6 x+7=0 .$ Không giải phương trình, hãy tính tổng và tích của hai nghiệm của phương trình đó.
a, Do \(x=-4\)là một nghiệm của pt trên nên
Thay \(x=-4\)vào pt trên pt có dạng :
\(16+4m-10m+2=0\Leftrightarrow-6m=-18\Leftrightarrow m=3\)
Thay m = 3 vào pt, pt có dạng : \(x^2-3x-28=0\)
\(\Delta=9-4.\left(-28\right)=9+112=121>0\)
vậy pt có 2 nghiệm pb : \(x_1=\frac{3-11}{2}=-\frac{8}{2}=-4;x_2=\frac{3+11}{2}=7\)
b, Theo Vi et : \(\hept{\begin{cases}x_1+x_2=-\frac{b}{a}=6\\x_1x_2=\frac{c}{a}=7\end{cases}}\)
Vậy m=3, và ngiệm còn lại x2=7
a)
m = 3
x2=7
Không dùng công thức nghiệm, tính tích các nghiệm của phương trình 3 x 2 – 10 x + 3 = 0
A. 3
B. 10 3
C. 1
D. -1
Ta có:
3x2 – 10x + 3 = 0 ⇔ 3x2 – 9x − x + 3 = 0
⇔ 3x (x – 3) – (x – 3) = 0
⇔ (3x – 1) (x – 3) = 0
⇔ 3 x − 1 = 0 x − 3 = 0 ⇔ x = 1 3 x = 3
Nên tích các nghiệm của phương trình là 1 3 .3 = 1
Đáp án cần chọn là: C
Cho phương trình 7 x 2 + 2 ( m – 1 ) x - m 2 = 0 .
a) Với giá trị nào của m thì phương trình có nghiệm?
b) Trong trường hợp phương trình có nghiệm, dùng hệ thức Vi-ét, hãy tính tổng các bình phương hai nghiệm của phương trình theo m.
a) Ta có: a = 7, b= 2(m-1), c = - m 2
Suy ra: Δ ' = ( m - 1 ) 2 + 7 m 2
Do ( m - 1 ) 2 ≥ 0 mọi m và m 2 ≥ 0 mọi m
=> ∆’≥ 0 với mọi giá trị của m.
Do đó phương trình có nghiệm với mọi giá trị của m.
b) Gọi hai nghiệm của phương trình là x 1 ; x 2 .
Theo định lý Vi-et ta có: 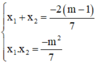
Khi đó:
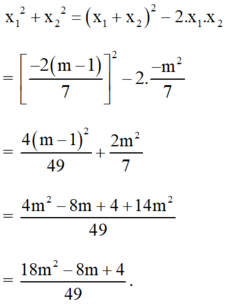
Cho phương trình 7x2 + 2(m – 1)x - m2 = 0
Trong trường hợp phương trình có nghiệm, dùng hệ thức Vi-ét, hãy tính tổng các bình phương hai nghiệm của phương trình theo m.
Gọi hai nghiệm của phương trình là x1; x2.
Theo định lý Vi-et ta có: 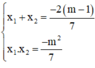
Khi đó:
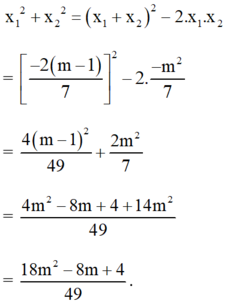
Cho phương trình 7x^2 + 2(m-1)x - m^2 = 0
a) Với giá trị nào của m thì phương trình có nghiệm?
b) Trong trường hợp phương trình có nghiệm, dùng hệ thức Vi-ét, hãy tính tổng các bình phương hai nghiệm của phương trình theo m
phương trình có a = 7 khác 0 => là phương trình bậc 2
vậy phương trình có nghiệm <=> \(\Delta'\ge0\Leftrightarrow\left(m-1\right)^2-7.\left(-m^2\right)\ge0\Leftrightarrow\left(m-1\right)^2+7m^2\ge0\)(thỏa mãn với mọi m)
b) theo vi et ta có
+) x1+x2 = -b/a = 2(m-1)/7
+) x1.x2 = c/a = -m2/7
a) Ta có : a = 7 ; b = 2(m-1) ; c = -m2
\(\Rightarrow\Delta'=\left(m-1\right)^2+7m^2\)
Do \(\left(m-1\right)^2\ge0\)mọi m và \(m^2\ge0\)mọi m
\(\Rightarrow\Delta'\ge0\)với mọi giá trị của m
Do đó PT có nghiệm với mọi giá trị của m
b) Gọi 2 nghiệm của PT là x1 ; x2
Theo định lí Vi-ét , ta có : \(\hept{\begin{cases}x_1+x_2=\frac{-2\left(m-1\right)}{7}\\x_1.x_2=\frac{-m^2}{7}\end{cases}}\)
Khi đó : \(x_1^2+x_2^2=\left(x_1+x_2\right)^2-2.x_1.x_2\)
\(=\left[\frac{-2\left(m-1\right)}{7}\right]^2-2.\frac{-m^2}{7}\)
\(=\frac{4\left(m-1\right)^2}{49}+\frac{2m^2}{7}\)
\(=\frac{4m^2-8m+4+14m^2}{49}\)
\(=\frac{18m^2-8m+4}{49}\)