Cho u → 0,5 và A(2,0). Ảnh của A qua phép tịnh tiến theo véctơ u → có toạ độ là:
A. (0,0)
B. (2;5)
C.(2;0)
D.(2;–5)
Những câu hỏi liên quan
Cho v → ( 2 ; 3 ) và A(–3;1). Ảnh của A qua phép tịnh tiến theo véctơ v → có toạ độ là:
A. (2;5)
B. (5;2)
C.(4;1)
D. (–1;4)
Cho
v
→
1
;
1
và
A
0
;
−
1
. Ánh của A qua phép tịnh tiến theo véctơ
v
→
có toạ độ là: A.
1
;
0
B.
0
;...
Đọc tiếp
Cho v → 1 ; 1 và A 0 ; − 1 . Ánh của A qua phép tịnh tiến theo véctơ v → có toạ độ là:
A. 1 ; 0
B. 0 ; 1
C. 1 ; 2
D. 2 ; 1
Đáp án A
Áp dụng biểu thức x ' = x + a y ' = y + b
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy cho véctơ
v
→
(
1
;
-
2
)
và điểm A(3;1). Ảnh của điểm A qua phép tịnh tiến theo véctơ
v
→
là điểm A có tọa độ A. A(-2;-3) B. A(2;-3) C. A(4;-1) D. A(-1;4)
Đọc tiếp
Trong mặt phẳng tọa độ Oxy cho véctơ v → = ( 1 ; - 2 ) và điểm A(3;1). Ảnh của điểm A qua phép tịnh tiến theo véctơ v → là điểm A' có tọa độ
A. A'(-2;-3)
B. A'(2;-3)
C. A'(4;-1)
D. A'(-1;4)
Trong mặt phẳng tọa độ Oxy cho véctơ
v
→
l
;
−
2
và điểm
A
3
;
1
.
Ảnh của điểm A qua phép tịnh tiến theo véctơ
v
→
là điểm A có tọa độ A.
A
−
2...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy cho véctơ v → = l ; − 2 và điểm A 3 ; 1 . Ảnh của điểm A qua phép tịnh tiến theo véctơ v → là điểm A' có tọa độ
A. A ' − 2 ; − 3
B. A ' 2 ; 3
C. A ' 4 ; − 1
D. A ' − 1 ; 4
Đáp án C
Ta có:
T v → A = A ' ⇒ A A ' = v → ⇔ x A ' - 3 = 1 y A ' - 1 = 2 ⇔ A ' 4 ; - 1
Đúng 0
Bình luận (0)
Trong mặt phẳng với hệ toạ độ Oxy cho véctơ
v
→
(-1;2) điểm A(3;5). Tìm tọa độ của các điểm A là ảnh của A qua phép tịnh tiến theo
v
→
. A. A(2;7) B. A(-2;7) C. A(7;2) D. A(-2;-7)
Đọc tiếp
Trong mặt phẳng với hệ toạ độ Oxy cho véctơ v → (-1;2) điểm A(3;5). Tìm tọa độ của các điểm A' là ảnh của A qua phép tịnh tiến theo v → .
A. A'(2;7)
B. A'(-2;7)
C. A'(7;2)
D. A'(-2;-7)
Cho đường tròn (C): x^2 + y^2 −3x+4y−5= 0 và véctơ u (−2;4). Tìm ảnh của đường tròn (C) qua phép tịnh tiến theo véctơ u ! giải hộ vs
gọi M(x,y) là 1 điểm thuộc (C) , M'(x';y') thuộc ảnh của (C) là ảnh của M qua phép tịnh tiến theo vecto u
=> \(\hept{\begin{cases}x'-x=-2\\y'-y=4\end{cases}}\Rightarrow\hept{\begin{cases}x=x'+2\\y=y'-4\end{cases}}\\ \)
thay x,y vào pt đường tròn (C)=> \(\left(x'+2\right)^2+\left(y'-4\right)^2-3\left(x'+2\right)+4\left(y'-4\right)-5=0\)
=> \(x'^2+4x'+4+y'^2-8y'+16-3x'-6+4y'-16-5=0\)
=>\(x'^2+x'+y'^2-4y'-7=0\)=>\(\left(x'+\frac{1}{2}\right)^2+\left(y'-2\right)^2=\frac{45}{4}\)
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy cho vectơ
v
→
-
1
;
2
,
A
3
;
5
,
B
-
1
;
1
và đường thẳng d có phương trình
x
–
2...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy cho vectơ v → = - 1 ; 2 , A 3 ; 5 , B - 1 ; 1 và đường thẳng d có phương trình x – 2 y + 3 = 0 .
a. Tìm tọa độ của các điểm A' , B' theo thứ tự là ảnh của A, B qua phép tịnh tiến theo vecto v →
b. Tìm tọa độ của điểm C sao cho A là ảnh của C qua phép tịnh tiến theo vectơ v →
c. Tìm phương trình của đường thẳng d' là ảnh của d qua phép tịnh tiến theo v .
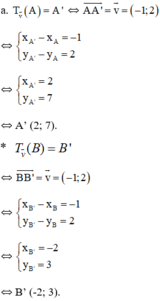
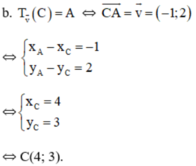
c) Đường thẳng d có vecto pháp tuyến là n→(1;-2) nên 1 vecto chỉ phương của d là(2; 1)
=> Vecto v→ không cùng phương với vecto chỉ phương của đường thẳng d
=> Qua phép tịnh tiến v→ biến đường thẳng d thành đường thẳng d’ song song với d.
Nên đường thẳng d’ có dạng : x- 2y + m= 0
Lại có B(-1; 1) d nên B’(-2;3) d’
Thay tọa độ điểm B’ vào phương trình d’ ta được:
-2 -2.3 +m =0 ⇔ m= 8
Vậy phương trình đường thẳng d’ là:x- 2y + 8 = 0
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, biết điểm M’(-3;0) là ảnh của điểm M(1;-2) qua phép tịnh tiến theo vectơ
u
→
và M”(2;3) là ảnh của điểm M’ qua phép tịnh tiến theo vectơ
v
→
. Tìm tọa độ vectơ
u
→
+
v
→
. A. (1;5) B. (-4;2) C. (5;3) D. (0;1)
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, biết điểm M’(-3;0) là ảnh của điểm M(1;-2) qua phép tịnh tiến theo vectơ u → và M”(2;3) là ảnh của điểm M’ qua phép tịnh tiến theo vectơ v → . Tìm tọa độ vectơ u → + v → .
A. (1;5)
B. (-4;2)
C. (5;3)
D. (0;1)
Trong mặt phẳng tọa độ Oxy, biết điểm
M
−
3
;
0
là ảnh của điểm
M
1
;
−
2
qua phép tịnh tiến theo vectơ
u
→
và
M
2...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, biết điểm M ' − 3 ; 0 là ảnh của điểm M 1 ; − 2 qua phép tịnh tiến theo vectơ u → và M ' ' 2 ; 3 là ảnh của điểm M ' ' 2 ; 3 qua phép tịnh tiến theo vectơ v → . Tìm tọa độ vectơ u → + v → .
A. 1 ; 5 .
B. − 4 ; 2 .
C. 5 ; 3 .
D. 0 ; 1 .
Đáp án A
Ta có u → = M M ' → = − 4 ; 2 . v → = M ' M ' ' → = 5 ; 3
Vậy u → + v → = 1 ; 5
Đúng 0
Bình luận (0)