Chứng tỏ đường thẳng đi qua trung điểm của hình thang cân là trục đối xứng của hình thang cân
Những câu hỏi liên quan
cmr đường thẳng đi qua hình thang cân là trục đối xứng của hình thang cân đó
Thế nào là hai điểm đối xứng với nhau qua một đường thẳng? Trục đối xứng của hình thang cân là đường thẳng nào?
- Hai điểm gọi là đối xứng với nhau qua đường thẳng d nếu d là đường trung trực của đoạn thẳng nối hai điểm đó.
- Trục đối xứng của hình thang cân là đường thẳng đi qua trung điểm hai đáy của hình thang cân.
Đúng 0
Bình luận (0)
Thế nào là hai điểm đối xứng với nhau qua một đường thẳng ? Trục đối xứng của hình thang cân là đường thẳng nào ?
Hai điểm gọi là đối xứng với nhau qua đường thẳng d nếu d là đường trung trực của đoạn thẳng nối hai điểm đó. Đường thẳng đi qua trung điểm hai đáy của hình thang cân là trục đối xứng của hình thang đó.
Đúng 0
Bình luận (0)
Hai điểm gọi là đối xứng với nhau qua đường thẳng d nếu d là đường trung trực của đoạn thẳng nối hai điểm đó. Đường thẳng đi qua trung điểm hai đáy của hình thang cân là trục đối xứng của hình thang đó.
Đúng 0
Bình luận (0)
Cho hình thang cân ABCD (AB // CD). Gọi O là giao điểm của 2 đường chéo, I là trung điểm của hình thang. Chứng minh OI là trục đối xứng của hình thang
Chứng minh rằng giao điểm hai đường chéo hình thang cân nằm trên trục đối xứng của hình thang cân.
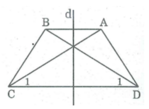
Hình thang cân ABCD có AB // CD
Gọi O là giao điểm của hai đường chéo AC và BD.
Xét ∆ ADC và ∆ BCD:
AD = BC (tính chất hình thang cân)
AC = BD (tính chất hình thang cân)
CD chung
Do đó ∆ ADC= ∆ BCD (c.c.c)
⇒ ∠ D 1 = ∠ C 1
⇒ ∆ OCD cân tại O
⇒ OC = OD nên O nằm trên đường trung trực của CD.
Trục đối xứng hình thang cân là đường thẳng trung trực của hai đáy.
Vậy O thuộc trục đối xứng của hình thang cân.
Đúng 0
Bình luận (0)
a) Em hãy chứng tỏ phát biểu sau đây là sai:
"Nếu một hình thang có hai cạnh bên bằng nhau thì đó là hình thang cân"
b) Cho tam giác ABC có ba góc nhọn.Gọi O là trung điểm của BC.Gọi D là điểm đối xứng của A qua BC;E là điểm đối xứng của A qua O.
Chứng minh rằng BCED là hình thang cân.
Chứng minh rằng giao điểm hai đường chéo của hình thang cân nằm trên trục đối xứng của hình thang cân ?
Chứng minh rằng giao điểm hai đường chéo của hình thang cân nằm trên trục đối xứng của hình thang cân
Gọi O là giao điểm hai đường chéo AC,BD của hình thang cân
Xét tam giác ADC và tam giác BCD ta có:
AD=BC
góc ADC=góc BCD
DC chung
=> tam giác ADC=tam giác BCD (c-g-c)
=> góc ACD=góc BDC
=> tam giác COD cân tại O => OD=OC
=> O thuộc đường trung trực của CD
=> O thuộc trục đối xúng của hình thang cân
Đúng 0
Bình luận (0)
Cho hình thang can ABCD M và N là trung điểm của hai đáy I và K là trung điểm của hai cạnh bên vẽ hình đối xứng của hình thang cân trên qua 2 đường thẳng MN và IK
Vẽ hình thang cân:
Cho trước ba điểm A, B, C. Dựng đỉnh D của hình thang cân ABCD dựa trên các công cụ đoạn thẳng, đường trung trực và phép biến đổi đối xứng qua trục.
Đặc điểm hình thang cân:
AD // BC, AB = CD
d là đường trung trực BC thì d cũng là đường trung trực cạnh AD
Các bước vẽ hình thang cân:
Sử dụng công cụ tạo điểm mới để tạo ba điểm A, B, C.
Sử dụng công cụ đường trung trực vẽ đường trung trực của cạnh BC
Sử dụng công cụ đối xứng vẽ điểm đối xứng của A qua trục đối xứng
Đúng 0
Bình luận (0)